TopView Transformation (鳥瞰図変換) 1
いよいよつくばチャレンジに向けての具体的な”ロボット工作”的投稿です.突然ですが,最近の車についてるアラウンドビューモニタってご存じですか?駐車しようとしたときに,ナビに表示される車全体を上から見たような絵のことです.
自分は画像処理の経験が浅いからかもしれませんが,これって本当にすごいと思います.実際にはカメラは車両のバンパやサイドミラーに”斜め下向き”についているので,カメラから得られる画像そのものはもちろんトップビューではないんですが,カメラと車の正確な位置情報をつかってえられた画像を変換してやることで,まるで地面を上から見ているような映像に変えることができるわけです.
で,これがつくばチャレンジのロボットとなんの関係があるの?という話なんですが,ロボットの自己位置推定にトップビュー変換した画像を使えないかと考えているわけです.流れとしては,,,,
①手動で,つくばチャレンジ2016のコース上をロボット走行させる.
②走行中,適切な間隔で写真を撮っていく.
③走行後,撮影した写真を Top View 変換する.
①~③のステップで,理想的な走行経路から撮影した Top View 画像が取得できます.自動で走らせるときには,この事前に撮りためた Top View 画像と今まさに取得している写真の Top View 画像の比較をして,自動走行時のロボットがどこにいるかを判断します.
(上手くいくかどうかわかりませんが...)
ということで,まず Top View 変換のプログラムを作ることにしました.OpenCV の WarpAffine という関数を呼べば割と簡単に作れそうだったのですが,とりあえず肝になるところだと思ったので勉強がてら論文読み&サンプルコードを実装してみます.
文献
参考にしたのは,下記の文献です.
- Vehicle Detection Based on Perspective Transformation Using Rear-View Camera
- A Vision Based Top-View Transformation Model for a Vehicle Parking Assistant
- 鳥瞰表示による駐車支援システム
技術概要
Vehicle Detection Based on Perspective Transformation Using Rear-View Camera で用いられていた下記の図がわかりやすかったので,この図をベースに考えていきます.
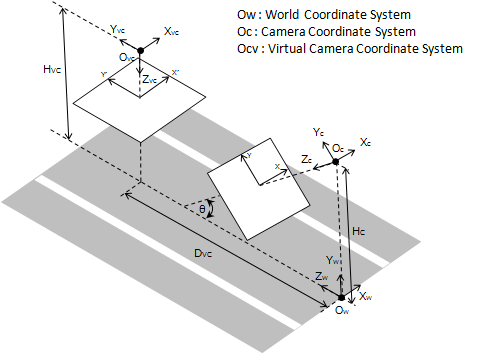
座標変換
視点変換をするにあたり,まずは座標変換を考えないといけません.いきなり撮像面間 (xy平面 - x'y'平面) の変換を考えるとこんがらがるので,カメラセンター座標間 (Oc座標 - Ovc座標) の変換を考えるところから始めます.元々のカメラ位置は Oc にあるわけですが,ここから見える風景を,あたかも Ovc から見たように変換する必要があります.つまり,「Oc から見た時の風景の各点の 3次元座標を,Ovcから見た時の 3次元座標に変換する」必要があるわけです.
上記は空間内の一点で,それを世界座標系 から見た座標とします.カメラ座標系
,仮想カメラ座標系
から見たそれぞれの座標を下記のように定義します.
また,仮想カメラ座標系から見たカメラ座標系の位置関係は下記のようになります.
回転関係 :
並進関係 :
上記の回転関係と並進関係を用いると,座標間の関係性は下記の変換行列で結ばれます.
上記をそのまま計算すると,下記の 3 つの関係式が導かれます.
1.
2.
※変換後のZ座標は常に なので,上記の最後の式は最終的には下記のようになります.
3.
また,三次元座標と投影座標の関係より,下記の 4 式が導かれます.
Camera ピクセル座標系
4.
5.
Virtual Camera ピクセル座標系
6.
7.
上記の 7 つの式から, を消去すると,論文に乗っている下記の式を得ることができます.
ふー...やっとまとまりました.最後の 2 式の変換を実際に実装していきます.
TopView Transformation 2 を好ご期待!!