カメラの位置・姿勢推定2 PNP問題 理論編
引き続きカメラの位置・姿勢推定問題です.PNP問題の解き方をまとめます.
問題分類のエントリで書いたように,下記を前提とします.
前提条件1:カメラの内部パラメータがわかっている.
前提条件2:基準となる座標系(ワールド座標系)が定義されており,撮影する物体(の各点)のワールド座標系での位置が事前に分かっている.
問題設定
解こうとしている問題のイメージ
上記の前提を図示してみると,下記のようなイメージかと思います.ここで,Xiは各点のワールド座標系での位置,xiはその各点をカメラで撮影した時の画像座標系での投影点です.
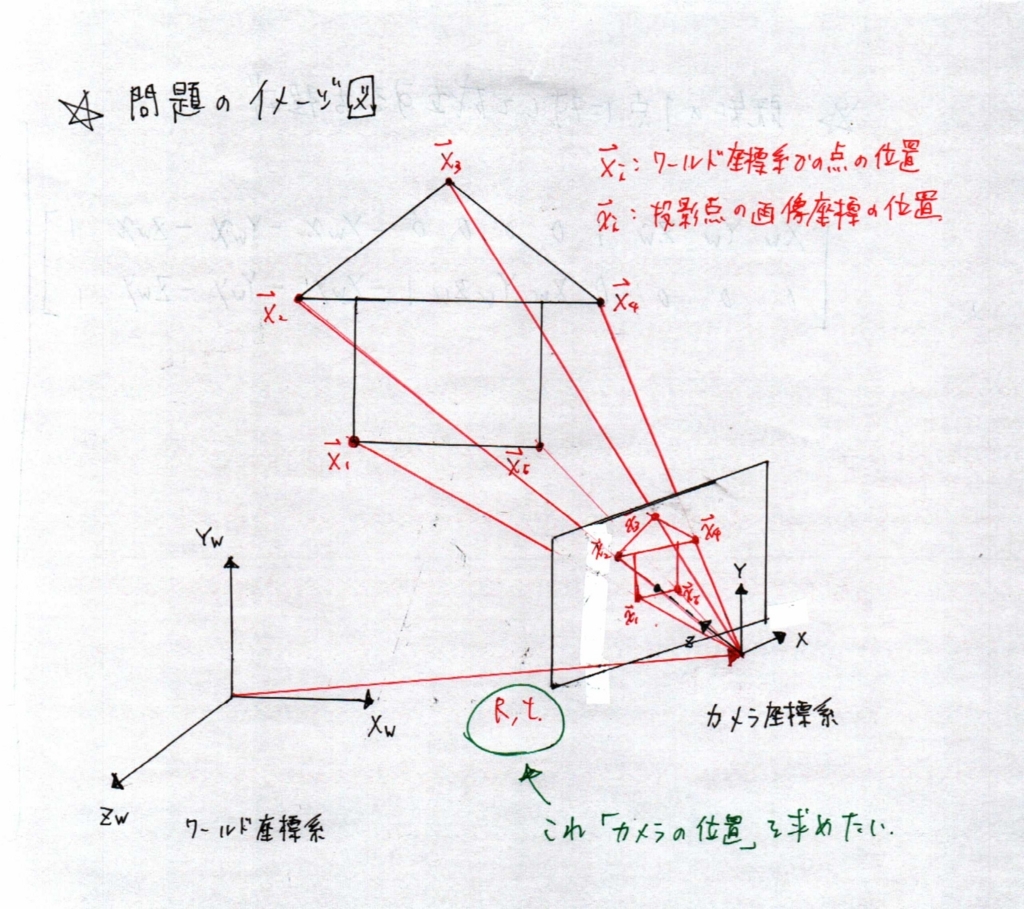
家の頂点五点が赤く塗られていますが,この頂点のワールド座標系での位置が分かっているとします.この時にカメラで撮った家の写真をみて,「この写真をとったカメラの位置は?」を求めるのがこの問題です.ちなみに,上記の絵に記載されている「R, t」がカメラの位置になります.
アルゴリズムのINとOUT
アルゴリズムに対するINとOUTは下記になります.

ちなみに,ノートに赤字で書いていますが,カメラ姿勢が自由度6(並進3と回転3)なので,3点(x と y のペア)が既知ならば,不定性は残るものの原理的にはカメラの位置が求まります.これをP3P問題といいます.P3P問題を解くアルゴリズムは Three Point Algorithm と呼ばれているようです.6点あれば線形の方程式を解く問題に帰着できてこれをP6P問題といいます.
P3P問題は非線形方程式を解く必要があり複雑なので,ここではP6P問題の解き方を説明していきます.今回の例のように6点を用いてDLT法で方程式を解いた場合,変数の消去をしなくてもいいので比較的簡単に解けます.
問題解決までの流れ
実際にカメラの位置を求めるには,大きく分けて二つのステップを経る必要があります.
1.DLT法を用いて透視投影行列を求める.
2.透視投影行列を R, t に分解する.
1.DLT法を用いて透視投影行列を求める.
方程式
解くべき方程式は,斉次座標表現を用いて下記のようにあらわされます.

ここで,上式は斉次座標表現を用いて表されており,「定数倍を許して等しいとみなす」のでした.しかしながら,カメラの位置はこの「定数倍」もはっきりさせないと一意に決めることができません.そのため,方程式を解くためにもう一つの変数も導入します.

この問題設定では,上記の方程式で既知の値と未知の値は下記のようになります.
既知の値:
「ワールド座標系での点座標(Xi, Yi, Zi, 1)」
「正規化画像座標系での投影点座標(xi, yi, zi, 1)」
未知の値:
「透視投影行列(カメラ行列)の各要素12個(pij)」
「新たに導入した定数倍ファクター λi」
透視投影行列は12個の要素を持ちますが,実際には定数倍を許して等しいとみなすので,自由度は11です.また,点が一つ増えることに定数倍ファクターのλiが一つ増えていきます.つまり,未知数と方程式の関係は下記のようになります.
既知の点ペア1つがもたらす線形方程式の個数:3
既知の点ペア1つがもたらす未知数の個数:1
透視投影行列の未知数:11
上記より,下記の条件が満たされれば線形方程式が解けます.
3N ≧ 11 + N
これを解くと,N ≧ 6となって,結果的に6点の対応関係がわかればカメラの位置が求まることになります.
DLT法を適用するための方程式展開
下記,方程式を展開して,DLT法が適用できるように Mx=b の形にします.下記のノートを見ていただければわかるように,この方程式では右辺が 0 になります.このような方程式を同次連立一次方程式(Homogeneous Linear Equations)といいます.

上式が1つの点が与える方程式です.この方程式が6つあれば,問題が解けることになります.N点が与えられた時の上記方程式を表すと,ベクトル表現と用いて下記のように表現できます.

だんだん数式が複雑になってきました....ここで,上記方程式の v を求めれば,透視投影行列が求まることになります.この数式は v = 0 が一つの解となることは自明ですが,明らかにこの解には興味がないので, v = 0 以外で上記の方程式を探します.つまり,v = 0 以外で,Mv が最小となる v を求めればよいことになります.また,透視投影行列には定数倍の不定性があり,要素は12個あるけれども,実際の自由度は11でした.このことより ||v|| = 1 という拘束条件をつけ足してあげると,この問題は下記のように表現できます.

係数行列 M を直行行列 U, V と対角行列 S を用いて表せました.ここで,問題は Mv = 0 (=|| Mv || がもっとも小さくなる v) となるような v を見つけることでしたので,特異値分解した行列 S から最小固有値を探せば,それに対応する固有ベクトルが v となります.
(このコラムでは特異値分解はちょっと触れられませんが,また別の機会にエントリを書きます.)
ふー.ここまでの計算で,透視投影がやっと求まりました.ただ,ここから R, t を求めなければ行けないので,もう一仕事です.
2.透視投影行列を R, t に分解する.
以前のエントリで説明しましたたが,透視投影行列と内部パラメータ行列,外部パラメータ行列の関係は下記のように表現されます.

ここまでの手順で,透視投影行列 P は求まっているので,P を分解して R, t の行列・ベクトルを求めることができれば,カメラの位置が分かったことになります.ここで,内部パラメータ行列 K が上三角行列であること,Rが回転行列であることを利用して RQ分解を使って P を分解します.

ここで,行列 A は透視投影行列 P を構成する 3x3 の行列であり,1のステップで既知です.なので,上記ノートの最後の行列式は R3 から順番に解いていくことができます.

次にR2を解きます.

最後にR1を解きます.

ここまでで,回転行列 R が求まりました.ここで,内部パラメータ行列 K の要素 (3, 3) は定義からは 1 となるはずですが,この手順のどこでもその条件を入れていないので, K の要素すべてを (3, 3) 要素で割ってあげれば内部パラメータ行列になります.t に関しては,内部パラメータ行列 K と並進ベクトル t からなる線形の方程式を解いてあげれば求まるかと思います.ということで,PNP問題の DLT 法を用いた解法でした.
