カメラの位置・姿勢推定2 PNP問題 実験編2
前回の下記エントリ,
daily-tech.hatenablog.com
では,OpenCVのSolvePNP関数を用いて世界座標が既知の7点,およびその投影点を用いてカメラ位置を計算しました.
今回のエントリでは,下記のブログでまとめたPNP問題の理論式をPythonで実装して同じことをやりたいと思います.
daily-tech.hatenablog.com
問題設定は実験編1と同じで下記のとおりです.
0.問題のイメージ図
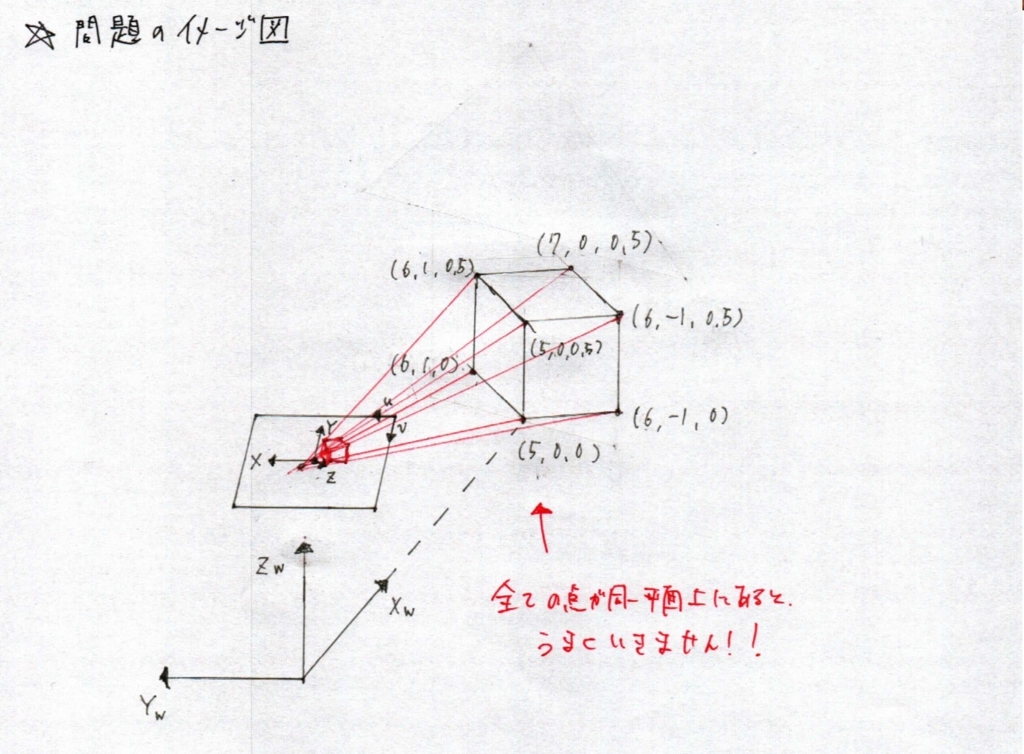
※すべての点が同一平面上にあると,下記のサンプルコードではうまくいきません!これではまって数週間....
1.世界座標が既知の7点を,位置が既知のカメラに投影した時の画像座標を求める.
ここでは,投影画像座標を求めます.問題を簡単にするために,画像にレンズひずみはないものとし,内部パラメータは下記のように定義します.
画像幅 :640pix
画像高さ:480pix
主点x :320
主点y :240
焦点距離:160pix
カメラ高さ:1m
カメラ角度:俯角30度
投影点は OpenCVの projectPoints 関数を使ってやれば簡単にできます.コードは実験編1を参照ください.
2.世界座標,画像座標が既知の点7点をつかってカメラの位置を求める
今度は上記の結果を使ってカメラ位置を求めます.下記は理論編で導いた数式を Python でコーディングしたものです.
import numpy as np
world = np.array(\
[\
( 5.00, 0.00, 0.00), \
( 5.00, 0.00, 0.50), \
( 6.00, -1.00, 0.00), \
( 6.00, -1.00, 0.50), \
( 6.00, 1.00, 0.00), \
( 6.00, 1.00, 0.50), \
( 7.00, 0.00, 0.50), \
])
img_pnt = np.array(\
[\
(320. , 294.12609945), \
(320. , 312.2071607), \
(291.91086401, 299.94150262), \
(290.62146125, 315.41433581), \
(348.08913599, 299.94150262), \
(349.37853875, 315.41433581), \
(320. , 317.74146755), \
])
f = 160
Cu = 320
Cv = 240
## Calculate Normalize Point
def calculateNormailzePnt(img_pnt):
normalized_img = np.zeros((0, 2))
for i in range(img_pnt.shape[0]):
vec = np.zeros((1, 2))
vec[0][0] = (img_pnt[i][0] - Cu) / f
vec[0][1] = (img_pnt[i][1] - Cv) / f
normalized_img = np.append(normalized_img, vec, axis = 0)
return normalized_img
## Create M Matrix that will be solved by SVD.
def createMMatrix(imgPnt, worldPnt):
pntNum = imgPnt.shape[0]
M = np.empty((0, 12 + pntNum))
for i in range(imgPnt.shape[0]):
Xw = worldPnt[i][0]
Yw = worldPnt[i][1]
Zw = worldPnt[i][2]
x = imgPnt[i][0]
y = imgPnt[i][1]
vec = np.zeros((3, 12 + pntNum))
# For X
vec[0, 0] = Xw
vec[0, 1] = Yw
vec[0, 2] = Zw
vec[0, 3] = 1.0
vec[0, 12 + i] = -x
# For Y
vec[1, 4] = Xw
vec[1, 5] = Yw
vec[1, 6] = Zw
vec[1, 7] = 1.0
vec[1, 12 + i] = -y
# For Z
vec[2, 8] = Xw
vec[2, 9] = Yw
vec[2, 10] = Zw
vec[2, 11] = 1.0
vec[2, 12 + i] = -1
M = np.append(M, vec, axis=0)
return M
def calculateProjectionMatrix(M):
U, S, V = np.linalg.svd(M, full_matrices=True)
num = 1
v = V[V.shape[0] - num]
#print()
#print("Eigen Value Matrix S : ")
#print(S)
#print()
#print("Eigen Vector Matrix V : ")
#print(V)
#print()
#print("Eigen Vector with Minimum Eigen Value : ")
#print(v)
lamda = v[V.shape[0] - num]
#print()
#print("Lamda with minimum Eigen Value : ")
#print(lamda)
# lamda has to be positive!
if (lamda < 0):
sign = -1
#print()
#print("Projection Matrix P : ")
P = sign * np.array([[v[0], v[1], v[2], v[3]], [v[4], v[5], v[6], v[7]], [v[8], v[9], v[10], v[11]]])
#print(P)
return P
def calculateRotationMatrixViaQRFactorization(P):
A1 = np.matrix(P[0, 0:3])
A2 = np.matrix(P[1, 0:3])
A3 = np.matrix(P[2, 0:3])
f = np.linalg.norm(A3)
R3 = A3 / f
e = A2 * R3.T
d = np.linalg.norm(A2 - e * R3)
R2 = (A2 - e * R3) / d
c = A1 * R3.T
b = A1 * R2.T
a = np.linalg.norm(A1 - b * R2 - c * R3)
R1 = (A1 - b * R2 - c * R3) / a
#print()
#print("Rotation Matrix R : ")
R = np.zeros((0, 3))
R = np.append(R, R1, axis=0)
R = np.append(R, R2, axis=0)
R = np.append(R, R3, axis=0)
#print(R)
K = np.matrix([[a, b, c], [0, d, e], [0, 0, f]])
return R, K
if __name__ == "__main__":
print("Solve PNP Problem!")
# 1. Calculate Normalize Coordinate.
normalized_img = calculateNormailzePnt(img_pnt)
#M = createMMatrix(normalized_img, world)
# 2. Create M Matrix that will be solved by SVD.
M = createMMatrix(img_pnt, world)
# 3. Calculate Projection Matrix
P = calculateProjectionMatrix(M)
# 4. Calculate R and K matrix via QR factorization.
R, K = calculateRotationMatrixViaQRFactorization(P)
print("Camera Intrisic Matrix")
print(K / K[2, 2])
print()
# 5. Translation found by P = [KR KT] -> T = inv(K) * P[:, 3]
print("Camera Translation : ")
print(np.linalg.inv(K) * np.matrix(P[:, 3]).T)
print()
print("Camera Rotation : ")
print(R)
最終的には,カメラの内部パラメータ行列 K と並進ベクトル T が下記のように求まります.
仮想的に設定した, f = 160, Cu = 320, Cv = 240 が求まっていることがわかります.また,位置と回転に関しても「カメラ座標系からみた世界座標」が正しく求まっています.
Camera Intrisic Matrix [[ 1.60000000e+02 1.21914379e-08 3.20000000e+02] [ 0.00000000e+00 1.60000000e+02 2.40000000e+02] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00]] Camera Translation : [[ -3.13782333e-11] [ -8.66025401e-01] [ 5.00000005e-01]] Camera Rotation : [[ -2.33381743e-10 1.00000000e+00 2.54500444e-11] [ 4.99999998e-01 9.46498690e-11 8.66025405e-01] [ 8.66025405e-01 2.14840023e-10 -4.99999998e-01]]