2画像間のホモグラフィー行列の計算
ということで,下記の魚眼カメラのキャリブレーションエントリからの「スピンオフ?」としてホモグラフィー行列の計算エントリを書き残します.
0.ホモグラフィー行列とは何か?
平面を撮影した2つの画像は射影変換と呼ばれる関係で結ばれます.って,これだけ書くと意味わかんないんで図を書いてみます.

3年前に画像処理を勉強し始めて本を読んだ時には,「で,それがなんなの?」と思ってたんですが,これって結構役に立ちます.大事なことは上述の「ホモグラフィー行列Hがわかっていれば,カメラAに写っているキャリブボードと同一平面上にある点のカメラBでの座標を計算できる」というところで,自動車に搭載されているアラウンドビューモニタなんかもこれを使ってます.(ちなみに,”同一平面に”というのがポイントで,同一平面上にない点は変なところに変換されます.)
日産HPのリンクを貼ってますが,この例だとカメラAが車両に搭載されているカメラで,カメラBが地面を真上から見ているカメラです.この場合にはカメラBはもちろん実際には存在しないので,カメラAとカメラBの位置関係から事前にホモグラフィー行列Hを計算しておいて,Hを使ってカメラAのビューを変換して車内に写してます.
1.ホモグラフィー行列の計算方法
で,どうやってHを計算すんのか?って話なんですが,毎度のことながらたくさんの線形方程式を解いて求めます.Hを求めるときにはカメラAで撮影した点の画像座標と,それに対応するカメラBで撮影した点の画像座標が必要になります.(つまり,上図のキャリブボード上の赤点のそれぞれの写真内での座標.)

ということで,スラスラーと書いてみたんですが,スラスラーと頭から出てきたわけではなく本にかじりついてます(笑).ホモグラフィー行列をかけた後に,ベクトルの外積が0になるところから方程式を導き出して...みたいなとこって数学得意な人ならすぐにおもいつくんですかね.ひとまず,上の導出でよく見る方程式の形 ”Ah = 0” が出てきました.これをもう少し具体的に書き下すと...

で,最後に書き下した数式なんですが,XB = [XB, YB, ZB] の z 座標であるZBでAを割ってあげても方程式が満たされます.なので,計算の単純化のためにXB = [XB / ZB, YB / ZB, 1] とします.こうすることで,取得した点 XB を正規化画像座標として扱います.
次に Ah = 0 の解である h を求めますが,求める解 h には定数倍の不定性があるので h33 = 1とするなり,|h| = 1 とするなりして適当に制約条件をつけてあげます.こうすることで,最終的に方程式は下記のようになります.

で,最後の方に Ah = 0 の最終的な形を書いていると思うんですが,4点あったらホモグラフィー行列自体は求まりますが,画像Aと画像Bの対応点自体に誤差が含まれるので実際にはキャリブレーションの時みたいにもっとたくさんの点を入力します.この点を元に行列式 A を作って,後は入力点に対して Ah がもっとも小さくなるような h を特異値分解で求めます.
実装(線形方程式を解いてホモグラフィー行列を求める.)
下記,実際の C++ での実装です.
Mat ComputeHomographyViaDLT(const Mat& pnt_to_be_projected, const Mat& pnt_destnation) { LOG(INFO) << "Inside \"ComputeHomographyViaDLT\""; // Build linear system L. int point_num = pnt_to_be_projected.cols; Mat L = Mat::zeros(2 * point_num, 9, CV_64FC1); for (int i = 0; i < point_num; ++i) { for (int j = 0; j < 3; j++) { L.at<double>(2 * i, j + 3) = pnt_to_be_projected.at<double>(j, i); L.at<double>(2 * i, j + 6) = -pnt_destnation.at<double>(1, i) * pnt_to_be_projected.at<double>(j, i); L.at<double>(2 * i + 1, j) = pnt_to_be_projected.at<double>(j, i); L.at<double>(2 * i + 1, j + 6) = -pnt_destnation.at<double>(0, i) * pnt_to_be_projected.at<double>(j, i); } } // Solve H via SVD. Mat H; { if (point_num > 4) { L = L.t() * L; } SVD svd(L); Mat h_vector = svd.vt.row(8) / svd.vt.row(8).at<double>(8); H = h_vector.reshape(1, 3); } return H; }
2.再投影誤差の最小化
1のホモグラフィー行列の計算でホモグラフィー行列自体は求まったのですが,線形の方程式を解いてあげるだけだとまだ投影誤差が少し大きいです.なので,非線形最適化を使って最終仕上げをします.
再投影誤差
で,最適化をするには誤差関数を作ってあげないといけないですが,今回の場合は下記のようになります.
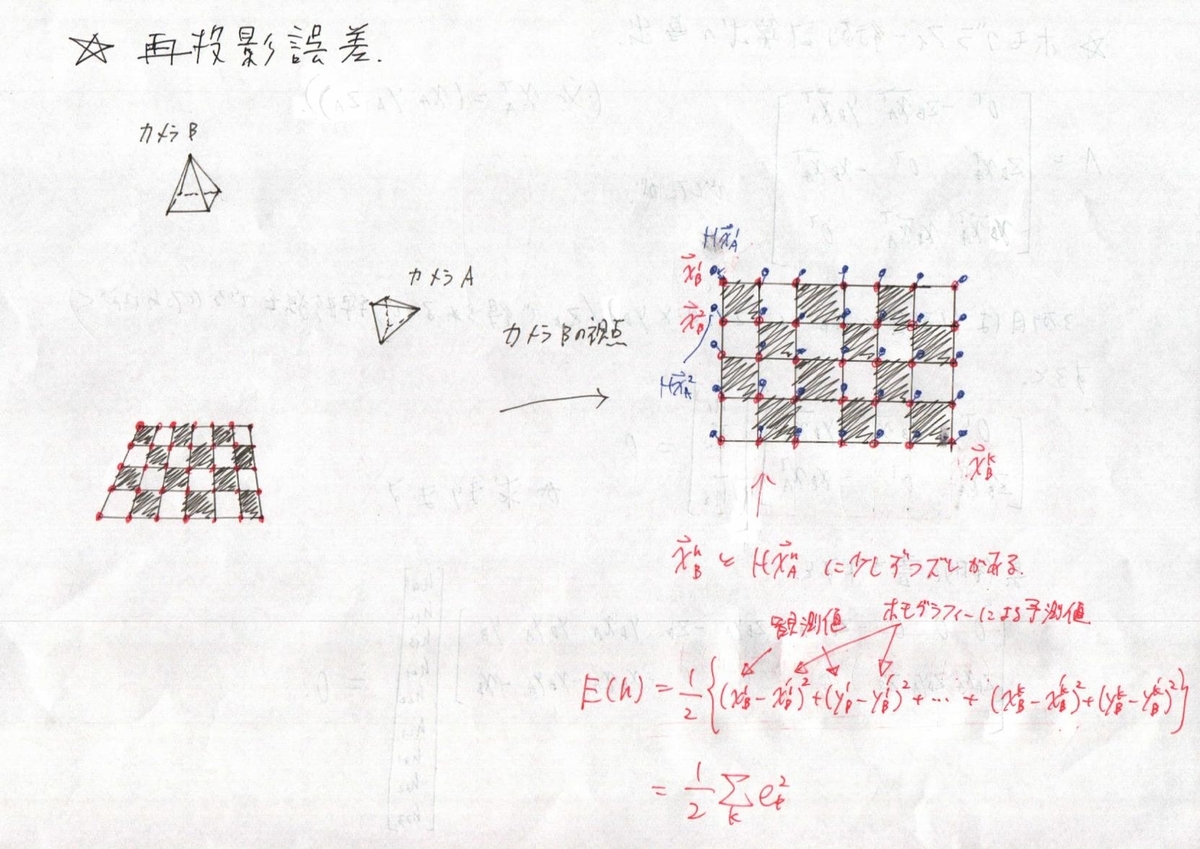
ヤコビアンの計算
ヤコビアンの計算ですが,今回の最適化では変動成分が H の各要素になります.これを一方で誤差関数の各要素 (ek) は個々のベクトル要素の差分になります. なので,これに対してヤコビアンを計算します.

で,上記の最後で誤差関数の各要素 ek が出てきましたが,結局ヤコビアンの要素は写像後の座標 xb, yb のそれぞれをホモグラフィー行列の要素で微分したものになります.

実装(ガウスニュートン法によるホモグラフィー行列の最適化)
void RefineHomographyViaGaussNewton(const Mat& pnt_to_be_projected, const Mat& pnt_destnation, const int iteration_num, Mat& H) { LOG(INFO) << "Inside \"RefineHomographyViaGaussNewton\""; int point_num = pnt_to_be_projected.cols; if (point_num > 4) { for (int iter = 0; iter < iteration_num; iter++) { Mat m_proj = H * pnt_to_be_projected; Mat m_reproj_err_vec, m_proj_normalized; double reproj_err; // Calculate Reprojection Error. { // Scale Adjustment. Dividing both side of eqn by m_proj.z. divide(m_proj, Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 2, m_proj.cols, 1)), m_proj_normalized); m_reproj_err_vec = m_proj_normalized(Rect(0, 0, m_proj_normalized.cols, 2)) - pnt_destnation(Rect(0, 0, pnt_destnation.cols, 2)); m_reproj_err_vec = Mat(m_reproj_err_vec.t()) .reshape(1, m_reproj_err_vec.cols * m_reproj_err_vec.rows); reproj_err = cv::norm(m_reproj_err_vec) / (double)point_num; } // Create Jacobian. Mat J = Mat::zeros(2 * point_num, 8, CV_64FC1); { Mat m_proj_z = m_proj(Rect(0, 2, m_proj.cols, 1)); Mat m_proj_z_2; multiply(m_proj_z, m_proj_z, m_proj_z_2); Mat MMM, MMM2, MMM3; divide(pnt_to_be_projected, Mat::ones(3, 1, CV_64FC1) * m_proj_z, MMM); multiply(Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 0, m_proj.cols, 1)), pnt_to_be_projected, MMM2); divide(MMM2, Mat::ones(3, 1, CV_64FC1) * m_proj_z_2, MMM2); multiply(Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 1, m_proj.cols, 1)), pnt_to_be_projected, MMM3); divide(MMM3, Mat::ones(3, 1, CV_64FC1) * m_proj_z_2, MMM3); for (int i = 0; i < point_num; ++i) { for (int j = 0; j < 3; ++j) { J.at<double>(2 * i, j) = MMM.at<double>(j, i); J.at<double>(2 * i + 1, j + 3) = MMM.at<double>(j, i); } for (int j = 0; j < 2; ++j) { J.at<double>(2 * i, j + 6) = -MMM2.at<double>(j, i); J.at<double>(2 * i + 1, j + 6) = -MMM3.at<double>(j, i); } } } // Update Homography Matrix H. { Mat h_vector = H.reshape(1, 9)(Rect(0, 0, 1, 8)).clone(); Mat dh_vec = -(J.t() * J).inv() * (J.t()) * m_reproj_err_vec; h_vector = h_vector + dh_vec; Mat tmp; vconcat(h_vector, Mat::ones(1, 1, CV_64FC1), tmp); H = tmp.reshape(1, 3); } LOG(INFO) << "Number of iteration : " << iter << ", Reproj Error : " << reproj_err << std::endl; } } }
実験結果
うーん.ちょっとDLTで求めたホモグラフィー行列の誤差がとても大きいです.ただ,最適化を実行すればすぐに誤差は収束したのですが,ひょっとするとDLTのあたりにバグがあるかもです.最終的な結果としては,,,
オリジナル画像1(この画像が変換する画像です.)

オリジナル画像2(この画像が変換が目指すべき画像です.)

最終的な全実装
結構気合を入れてエントリを作ったので,一式Githubにも上げておきます.ただ,1つのファイルでほぼすべてが完結するように書いてあるので,時間があればライブラリのリンクを通してあげれば下記でも動くかも...
/*M///////////////////////////////////////////////////////////////////////////// // // IMPORTANT: READ BEFORE DOWNLOADING, COPYING, INSTALLING OR USING. // // By downloading, copying, installing or using the software you agree to this // license. If you do not agree to this license, do not download, install, // copy or use the software. // // // License Agreement // For Open Source Computer Vision Library // // Copyright (C) 2000-2008, Intel Corporation, all rights reserved. // Copyright (C) 2009-2011, Willow Garage Inc., all rights reserved. // Third party copyrights are property of their respective owners. // // Redistribution and use in source and binary forms, with or without // modification, are permitted provided that the following conditions are met: // // * Redistribution's of source code must retain the above copyright notice, // this list of conditions and the following disclaimer. // // * Redistribution's in binary form must reproduce the above copyright // notice, this list of conditions and the following disclaimer in the // documentation and/or other materials provided with the distribution. // // * The name of the copyright holders may not be used to endorse or promote // products derived from this software without specific prior written // permission. // // This software is provided by the copyright holders and contributors "as is" // and any express or implied warranties, including, but not limited to, the // implied warranties of merchantability and fitness for a particular purpose // are disclaimed. In no event shall the Intel Corporation or contributors be // liable for any direct, indirect, incidental, special, exemplary, or // consequential damages (including, but not limited to, procurement of // substitute goods or services; // loss of use, data, or profits; or business interruption) however caused // and on any theory of liability, whether in contract, strict liability, // or tort (including negligence or otherwise) arising in any way out of // the use of this software, even if advised of the possibility of such damage. // //M*/ // System #include <algorithm> #include <fstream> #include <iostream> #include <vector> // Glog #include <glog/logging.h> // Gflag #include <gflags/gflags.h> // Boost #include <boost/algorithm/string.hpp> // OpenCV #include <opencv2/calib3d.hpp> #include <opencv2/core.hpp> #include <opencv2/highgui.hpp> #include <opencv2/imgproc.hpp> using namespace cv; namespace { void CreateHomogeneousPoints(const Mat& m, Mat& m_homo) { int point_num = m.cols; if (m.rows < 3) { vconcat(m, Mat::ones(1, point_num, CV_64FC1), m_homo); } else { m_homo = m.clone(); } divide(m_homo, Mat::ones(3, 1, CV_64FC1) * m_homo.row(2), m_homo); } void NormalizePoints(const Mat& pnt_homo, Mat& pnt_normalized, Mat& norm_mat, Mat& inv_norm_mat) { { Mat mx_row = pnt_homo.row(0).clone(); Mat my_row = pnt_homo.row(1).clone(); double mx_mean = mean(mx_row)[0]; double my_mean = mean(my_row)[0]; Mat normalized_mx_row = mx_row - mx_mean; Mat normalized_my_row = my_row - my_mean; double x_scale = mean(abs(normalized_mx_row))[0]; double y_scale = mean(abs(normalized_my_row))[0]; norm_mat = cv::Mat(Matx33d(1 / x_scale, 0.0, -mx_mean / x_scale, 0.0, 1 / y_scale, -my_mean / y_scale, 0.0, 0.0, 1.0)); inv_norm_mat = Mat(Matx33d(x_scale, 0, mx_mean, 0, y_scale, my_mean, 0, 0, 1)); pnt_normalized = norm_mat * pnt_homo; } } Mat ComputeHomographyViaDLT(const Mat& pnt_to_be_projected, const Mat& pnt_destnation) { LOG(INFO) << "Inside \"ComputeHomographyViaDLT\""; // Build linear system L. int point_num = pnt_to_be_projected.cols; Mat L = Mat::zeros(2 * point_num, 9, CV_64FC1); for (int i = 0; i < point_num; ++i) { for (int j = 0; j < 3; j++) { L.at<double>(2 * i, j + 3) = pnt_to_be_projected.at<double>(j, i); L.at<double>(2 * i, j + 6) = -pnt_destnation.at<double>(1, i) * pnt_to_be_projected.at<double>(j, i); L.at<double>(2 * i + 1, j) = pnt_to_be_projected.at<double>(j, i); L.at<double>(2 * i + 1, j + 6) = -pnt_destnation.at<double>(0, i) * pnt_to_be_projected.at<double>(j, i); } } // Solve H via SVD. Mat H; { if (point_num > 4) { L = L.t() * L; } SVD svd(L); Mat h_vector = svd.vt.row(8) / svd.vt.row(8).at<double>(8); H = h_vector.reshape(1, 3); } return H; } void RefineHomographyViaGaussNewton(const Mat& pnt_to_be_projected, const Mat& pnt_destnation, const int iteration_num, Mat& H) { LOG(INFO) << "Inside \"RefineHomographyViaGaussNewton\""; int point_num = pnt_to_be_projected.cols; if (point_num > 4) { for (int iter = 0; iter < iteration_num; iter++) { Mat m_proj = H * pnt_to_be_projected; Mat m_reproj_err_vec, m_proj_normalized; double reproj_err; // Calculate Reprojection Error. { // Scale Adjustment. Dividing both side of eqn by m_proj.z. divide(m_proj, Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 2, m_proj.cols, 1)), m_proj_normalized); m_reproj_err_vec = m_proj_normalized(Rect(0, 0, m_proj_normalized.cols, 2)) - pnt_destnation(Rect(0, 0, pnt_destnation.cols, 2)); m_reproj_err_vec = Mat(m_reproj_err_vec.t()) .reshape(1, m_reproj_err_vec.cols * m_reproj_err_vec.rows); reproj_err = cv::norm(m_reproj_err_vec) / (double)point_num; } // Create Jacobian. Mat J = Mat::zeros(2 * point_num, 8, CV_64FC1); { Mat m_proj_z = m_proj(Rect(0, 2, m_proj.cols, 1)); Mat m_proj_z_2; multiply(m_proj_z, m_proj_z, m_proj_z_2); Mat MMM, MMM2, MMM3; divide(pnt_to_be_projected, Mat::ones(3, 1, CV_64FC1) * m_proj_z, MMM); multiply(Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 0, m_proj.cols, 1)), pnt_to_be_projected, MMM2); divide(MMM2, Mat::ones(3, 1, CV_64FC1) * m_proj_z_2, MMM2); multiply(Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 1, m_proj.cols, 1)), pnt_to_be_projected, MMM3); divide(MMM3, Mat::ones(3, 1, CV_64FC1) * m_proj_z_2, MMM3); for (int i = 0; i < point_num; ++i) { for (int j = 0; j < 3; ++j) { J.at<double>(2 * i, j) = MMM.at<double>(j, i); J.at<double>(2 * i + 1, j + 3) = MMM.at<double>(j, i); } for (int j = 0; j < 2; ++j) { J.at<double>(2 * i, j + 6) = -MMM2.at<double>(j, i); J.at<double>(2 * i + 1, j + 6) = -MMM3.at<double>(j, i); } } } // Update Homography Matrix H. { Mat h_vector = H.reshape(1, 9)(Rect(0, 0, 1, 8)).clone(); Mat dh_vec = -(J.t() * J).inv() * (J.t()) * m_reproj_err_vec; h_vector = h_vector + dh_vec; Mat tmp; vconcat(h_vector, Mat::ones(1, 1, CV_64FC1), tmp); H = tmp.reshape(1, 3); } LOG(INFO) << "Number of iteration : " << iter << ", Reproj Error : " << reproj_err << std::endl; } } } cv::Mat ComputeHomography(const Mat& m, const Mat& M, bool run_optimization, const int iteration_num) { // Convert input to homogeneous Mat. Mat m_homo, M_homo; CreateHomogeneousPoints(m, m_homo); CreateHomogeneousPoints(M, M_homo); // Calculation down here will be done based on normalized coord. Mat H_m_to_M; { // Normalize x and y coordinate to make homogeneous. Mat m_normalized, m_norm_mat, inv_m_norm_mat; NormalizePoints(m_homo, m_normalized, m_norm_mat, inv_m_norm_mat); Mat M_normalized, M_norm_mat, inv_M_norm_mat; NormalizePoints(M_homo, M_normalized, M_norm_mat, inv_M_norm_mat); // Compute initial homography matrix. Mat H_m_to_M_normalized = ComputeHomographyViaDLT(m_normalized, M_normalized); H_m_to_M = inv_m_norm_mat * H_m_to_M_normalized * M_norm_mat; H_m_to_M = H_m_to_M / H_m_to_M.at<double>(2, 2); { cv::Mat m_reproj; cv::Mat m_proj = H_m_to_M * m_homo; divide(m_proj, Mat::ones(3, 1, CV_64FC1) * m_proj(Rect(0, 2, m_proj.cols, 1)), m_proj); LOG(INFO) << "After DLT Cauclation. Reproj Error : " << cv::norm(M_homo.reshape(1, 1) - m_proj.reshape(1, 1)) / (double)m_proj.cols; } } if (run_optimization) { // Refine homography matrix via optimization. RefineHomographyViaGaussNewton(m_homo, M_homo, iteration_num, H_m_to_M); } return H_m_to_M; } void LoadDetectPointsFromFile(const std::string& path, std::vector<cv::Point2d>& detected_points) { detected_points.clear(); std::ifstream reading_file(path, std::ios::in); CHECK(reading_file.is_open()) << "File at given path can not be opened." << path; while (!reading_file.eof()) { std::string line; std::getline(reading_file, line); std::vector<std::string> results; boost::split(results, line, [](char c) { return c == ','; }); if (results.size() != 2) { break; } detected_points.push_back( cv::Point2d(std::stod(results[0]), std::stod(results[1]))); } } void ConvertPoint2dToPoint2fVector(const std::vector<cv::Point2d>& src, std::vector<cv::Point2f>& dst) { dst.clear(); for (auto elem : src) { dst.push_back(cv::Point2f(elem.x, elem.y)); } } void ApplyHomographyMatToPoint2fVector(const std::vector<cv::Point2f>& src, std::vector<cv::Point2f>& dst, cv::Mat& H) { dst.clear(); for (auto elem : src) { cv::Mat pnt = (cv::Mat_<double>(3, 1) << elem.x, elem.y, 1.0); cv::Mat trans = H * pnt; dst.push_back(cv::Point2f(trans.at<double>(0, 0) / trans.at<double>(2, 0), trans.at<double>(1, 0) / trans.at<double>(2, 0))); } } } // namespace DEFINE_string(picture_path1, "/home/koichi/Desktop/Blog/Pic20190616/raw/DSC02719.jpg", "Path to the source picture."); DEFINE_string(picture_path2, "/home/koichi/Desktop/Blog/Pic20190616/raw/DSC02721.jpg", "Path to the source picture."); DEFINE_string(detection_result1, "/home/koichi/Desktop/Blog/Pic20190616/raw/DSC02719.txt", "Path to the detected corner location of image 1."); DEFINE_string(detection_result2, "/home/koichi/Desktop/Blog/Pic20190616/raw/DSC02721.txt", "Path to the detected corner location of image 2."); int main(int argc, char** argv) { google::ParseCommandLineFlags(&argc, &argv, true); FLAGS_alsologtostderr = 1; FLAGS_stderrthreshold = google::GLOG_INFO; google::InitGoogleLogging(argv[0]); // Read Picture. cv::Mat img1, img2; { img1 = cv::imread(FLAGS_picture_path1, CV_LOAD_IMAGE_COLOR); CHECK(!img1.empty()) << "Image 1 cannot be opened. " << FLAGS_picture_path1; img2 = cv::imread(FLAGS_picture_path2, CV_LOAD_IMAGE_COLOR); CHECK(!img2.empty()) << "Image 2 cannot be opened. " << FLAGS_picture_path2; } // Read std::vector<cv::Point2d> detected_point1, detected_point2; { LoadDetectPointsFromFile(FLAGS_detection_result1, detected_point1); LoadDetectPointsFromFile(FLAGS_detection_result2, detected_point2); } // Convert vector<cv::Point2f> to Mat cv::Mat point1_1ch, point2_1ch; { cv::Mat point1 = cv::Mat(detected_point1); cv::Mat temp[2]; cv::split(point1, temp); point1_1ch = cv::Mat::zeros(cv::Size(point1.rows, 2), CV_64FC1); point1_1ch.row(0) += temp[0].t(); point1_1ch.row(1) += temp[1].t(); cv::Mat point2 = cv::Mat(detected_point2); cv::split(point2, temp); point2_1ch = cv::Mat::zeros(cv::Size(point2.rows, 2), CV_64FC1); point2_1ch.row(0) += temp[0].t(); point2_1ch.row(1) += temp[1].t(); } // Compute homography. cv::Mat H_1_to_2_wo_opt, H_1_to_2_w_opt; { H_1_to_2_wo_opt = ComputeHomography(point1_1ch, point2_1ch, false, 0); H_1_to_2_w_opt = ComputeHomography(point1_1ch, point2_1ch, true, 50); LOG(INFO) << "H_1_to_2_wo_opt : " << H_1_to_2_wo_opt; LOG(INFO) << "H_1_to_2_w_opt : " << H_1_to_2_w_opt; } // Calculate Homography { cv::Mat warped_img_wo_opt, warped_img_w_opt; cv::Mat img2_with_corner = img2.clone(); cv::Mat img2_with_corner_wo_opt = img2.clone(); cv::Mat img2_with_corner_w_opt = img2.clone(); cv::warpPerspective(img1, warped_img_wo_opt, H_1_to_2_wo_opt, cv::Size(img1.cols, img1.rows)); cv::warpPerspective(img1, warped_img_w_opt, H_1_to_2_w_opt, cv::Size(img1.cols, img1.rows)); std::vector<cv::Point2f> detected_point1f, detected_point2f, warped_point2f_wo_opt, warped_point2f_w_opt; ConvertPoint2dToPoint2fVector(detected_point2, detected_point2f); cv::drawChessboardCorners(img2_with_corner, cv::Size(7, 10), detected_point2f, true); ConvertPoint2dToPoint2fVector(detected_point1, detected_point1f); ApplyHomographyMatToPoint2fVector(detected_point1f, warped_point2f_wo_opt, H_1_to_2_wo_opt); cv::drawChessboardCorners(img2_with_corner_wo_opt, cv::Size(7, 10), warped_point2f_wo_opt, true); ApplyHomographyMatToPoint2fVector(detected_point1f, warped_point2f_w_opt, H_1_to_2_w_opt); cv::drawChessboardCorners(img2_with_corner_w_opt, cv::Size(7, 10), warped_point2f_w_opt, true); cv::imshow("Image 1", img1); cv::imshow("Without Optimization", warped_img_wo_opt); cv::imshow("With Optimization", warped_img_w_opt); cv::imshow("Image 2 with DETECTED CORNER", img2_with_corner); cv::imshow("Image 2 with WARPED CORNER WITHOUT optimization", img2_with_corner_wo_opt); cv::imshow("Image 2 with WARPED CORNER WITH optimization", img2_with_corner_w_opt); cv::waitKey(0); } return 0; }



