制約のある軌道を生成する方法 〜 Constrained Trajectory Generation 〜
なかなか仰々しいタイトルになってしまいました(笑)
つくばチャレンジも終わりSFMに戻ろうかと思っていたのですが,今年のつくばチャレンジではなかなか愛犬が言うことを聞いてくれないこと(=Plannerの重要性)を痛感し,来年のために Planner 周りの勉強をしてます.で,せっかくなのである程度広く参考文献をあさってみたのですが,なかなかこれが自分には難しく...どうやってまとめればいいか...と思っている最中なんですが,ひとまず重要そうなトピックを小出しに書いてみることにしました.そこそこ部品ができてきたら大きなまとめを作れればと思ってます.
X.はじめに
人間が自動車を運転している状況を考えてみると,普通は進みたい軌道があると思います.例えば高速道路を走行しているときは,できれば走行レーンのど真ん中を走りたいですし,おしっこしたくなったら SA に入りたくなります.で,「走行レーンのど真ん中」とか「SAに入るためにレーンチェンジ」とかって,地球の表面を完全に x,y 平面だとすると,軌道は複数の点 (x, y) で定義されます.
が,実際に運転しているときにこの軌道を頭のなかで計算している人はいないと思います.しかも,実際に車を操作するときに使うインプットって,アクセル(≒加速度)とハンドル(≒角速度)ですよね?つまり,「走行レーンの真ん中を走る」というのは結果でしかなくて,走行レーンの真ん中からちょっとずれたらハンドルを逆に回して走行レーンの真ん中に戻す.という操作を繰り返して走行レーンの真ん中を走っています.
ロボットを制御するときも同じロジックで,レーンの真ん中からちょっとずれたらフィードバックして...という方法で制御することができます.自分は 2013年 にETロボコンというコンテストに出場したことがあるのですが,このロボコンのロボットは光センサーを使ったライントレースで目的地まで進んでいきます.このライントレースがここで言うフィードバックのイメージです.ロボットは進む方向も何も全くわかっておらず,自分の直下の黒線との位置関係だけをみて制御をしています.
(下記動画の最初の部分にライントレースしながら進むロボットが出てきます.)
が,この方法だとロボットの慣性が大きくなったり,緻密な制御が求められる場合に対応できなくなります.ETロボコンでも上位チームのロボットはめちゃ早いんですが(笑),速度が上がってくるとラインを追従しきれなくなってコースアウトするロボットも出てきてしまいます.
で,この問題を解決するためには,
「目標出力(走行レーンの真ん中を走る)を満たす入力(アクセル,ハンドル)を事前に計算して,そいつを入力する」
が必要になるわけですが,これが計算できれば,得られた値を入力として使うことによって,ある程度は期待に沿った目標出力が得られます.このエントリでは,目標出力を満たす入力を事前計算する方法をまとめたいと思います.
X.問題設定
ということで,具体的な問題設定をします.
出発点の車の状態
X_start = [xst, yst, φst, vst, θst]T
到達点の車の状態
X_end = [xend, yend, φend, vend, θend]T
x : 車両の x 座標
y : 車両の y 座標
φ : 車両の 向き
v : 車両の速度
θ : ステアリング角度(≒タイヤの切れ角)
上の2つがわかっている状況下で,2つの点をうまく繋いでくれる制御入力 [v, θ]T を求めます.ここでは,車両がレーンチェンジして停車するマヌーバを考えてみます.下図の点線のラインが,おそらく車両がたどるであろうラインです.

X.処理の大きな流れ
軌道生成法の大きなながれをまずクリアにして,それから各パートに入っていきたいと思います.このアルゴリズムで解く問題設定は下記のようになります.
1.制御入力をモデル化して関数として表現する.(v = f(t), θ = g(t))
2.モデル化関数のパラメータの初期値を決める.(v = av*t2 + bv*t + cv, θ = aθ*t2 + bθ*t + cθの,係数 a, b, c のこと.)
3.各時点での制御入力をモデル化関数から求め,数値積分して最終時間での車両状態を求め,到達点からの差分を計算する.(diff = X_end - X(tf))
4.到達点からの差分を,モデル化関数のパラメータに関して線形化してヤコビアンを計算する.
6.5で計算した修正ベクトルを使って,パラメータを更新し,3に戻る.
X.運動モデル
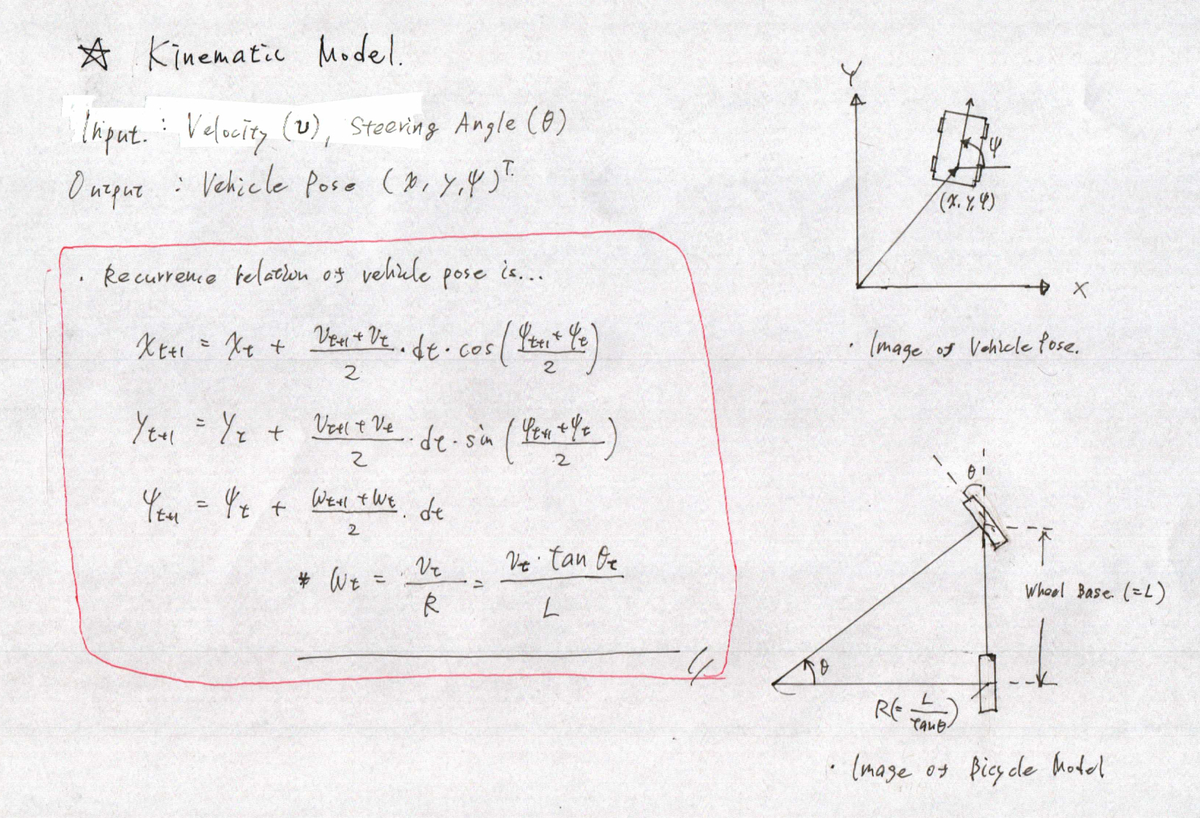
実際に入力から出力を計算するためには,制御対象となるロボットのモデルを考えてやる必要があります.自動車の例が一番イメージしやすいかと思ったので,二輪モデルを使って考えてみます.ここでは,入力と目標出力の関係は下記のように設定しました.
入力:速度(v),ステアリング角度(θ)
出力:車両の位置,向き(x, y, φ)
で,アクセルの場合は入力を加速度としたほうがよりイメージに近いかと思ったのですが,論文が速度入力だったので速度入力にしています.あと,ステアリング角とタイヤの切れ角は実際は違いますが,問題が複雑になるだけなので同じとしてます.
X.パラメータ化された制御入力(Parameterized Control Input)
今回のアプローチでは数値最適化を使います.なので,何らかの形で制御入力(v, θ)を数式に落としてあげないといけません.論文では,速度入力を時間に関しての台形関数,角速度を時間に関してのスプライン曲線で近似していたのですが,簡単のためにそれぞれを時間に関しての n次多項式としています.

ちなみに,論文では "Parameterized Vehicle Control" というワードが頻繁に出てきてたんですが,上図のように「入力を何らかの関数でモデル化して,そのパラメータ(上図だと,多項式の係数)として表現すること」なんですね.このイメージがなかなかわかずに「?」してました.
X.数値最適化を用いた最適パラメータの計算
ここからは最適化の導出をします.今回の最適化対象は,
X.実装
ということで,実装です.ごちゃごちゃとプロットや設定をしているとこがありますが,重要なとこは2つだけです.
収束計算を実施しているとこ.
下記の大きなループで収束計算を回しています.
for i in range(6):
v_coeffs = params[0: init_v_coeffs.shape[0]]
w_coeffs = params[init_v_coeffs.shape[0]: params.shape[0]]
# Forward Integration.
x_tf = b_traj.compute_states(x_init, v_coeffs, w_coeffs, t_st, t_end, dt)
# Plot Result of Forward Integration.
pose.plot(x_tf[0,:], x_tf[1,:], label="Iteration Count : " + str(i))
# Compute Jacobian via Linearization.
jaco = jacobian_calc.calc_jacobian(x_init, x_final, v_coeffs, w_coeffs, t_st, t_end, dt)
# Compute Parameter Correction Vector via Newton Methods
dx = np.append(x_init, x_final, axis=0) - np.append(x_tf[:,0], x_tf[:,-1], axis=0)
jaco_pseudo_inv = np.linalg.pinv(jaco)
dp = np.matmul(-jaco_pseudo_inv, dx)
params = params + dp
重要な箇所としては,
jacobian_calc.calc_jacobian(x_init, x_final, v_coeffs, w_coeffs, t_st, t_end, dt)
のラインでヤコビアンをつどつど計算して,その後の,
dx = np.append(x_init, x_final, axis=0) - np.append(x_tf[:,0], x_tf[:,-1], axis=0) jaco_pseudo_inv = np.linalg.pinv(jaco) dp = np.matmul(-jaco_pseudo_inv, dx) params = params + dp
のパートでパラメータ修正ベクトルを計算,パラメータの更新をしています
ヤコビアンを計算しているとこ
下記のパートでヤコビアンを計算しています.
def calc_jacobian(self, x_0, x_f, v_coeffs, w_coeffs, t_st, t_end, dt): jaco = np.zeros([x_0.shape[0] + x_f.shape[0], v_coeffs.shape[0] + w_coeffs.shape[0]]) params = np.append(v_coeffs, w_coeffs, axis=0) x_tgt = np.append(x_0, x_f, axis=0) for i in range(jaco.shape[1]): d = np.zeros(jaco.shape[1]) d[i] = self.__ep n_params = params - d p_params = params + d # Numerical Integration states = self.__b_traj.compute_states(x_0, n_params[0:v_coeffs.shape[0]], n_params[v_coeffs.shape[0]:params.shape[0]], t_st, t_end, dt) x_f_n = np.append(states[:, 0], states[:, -1], axis=0) states = self.__b_traj.compute_states(x_0, p_params[0:v_coeffs.shape[0]], p_params[v_coeffs.shape[0]:params.shape[0]], t_st, t_end, dt) x_f_p = np.append(states[:, 0], states[:, -1], axis=0) # Differentiation diff_n = x_tgt - x_f_n diff_p = x_tgt - x_f_p jaco[:, i] = (diff_p - diff_n) / (2*self.__ep) return jaco
今回のケースでは数値計算でヤコビアンを求めていますが,ヤコビアンの一つの列が一つのパラメータに対する変動成分を表すので,下記のコードをパラメータ数分実行してヤコビアンを作ってます.
d = np.zeros(jaco.shape[1]) d[i] = self.__ep n_params = params - d p_params = params + d # Numerical Integration states = self.__b_traj.compute_states(x_0, n_params[0:v_coeffs.shape[0]], n_params[v_coeffs.shape[0]:params.shape[0]], t_st, t_end, dt) x_f_n = np.append(states[:, 0], states[:, -1], axis=0) states = self.__b_traj.compute_states(x_0, p_params[0:v_coeffs.shape[0]], p_params[v_coeffs.shape[0]:params.shape[0]], t_st, t_end, dt) x_f_p = np.append(states[:, 0], states[:, -1], axis=0) # Differentiation diff_n = x_tgt - x_f_n diff_p = x_tgt - x_f_p jaco[:, i] = (diff_p - diff_n) / (2*self.__ep)
X.実験1(収束する場合)
実験結果は次のようになりました!出発点と到着点がそれぞれ色付きの丸で表されてまして,イテレーション毎に軌道が描かれてます.パラメータの初期値はすべて0からスタートさせましたが,このサンプルではいい感じに収束しました.二点,上述の説明と異なる部分がありまして,論文 ”Optimal rough terrain trajectory generation for wheeled mobile robots” では,速度,ステアリング角の初期条件は予め多項式の係数として事前に求めてから最適化を実施していましたが,そのロジックを作る代わりに初期状態と終了状態の両方のベクトルを制約条件として最適化しています.あと,レーンチェンジのマヌーバはステアリング操作が2次の多項式で表現できないため,速度,ステアリング角ともに3次の多項式にしてます.
走行開始時,走行終了時の両方の境界条件が満たされていることが下記のプロットから解ると思います.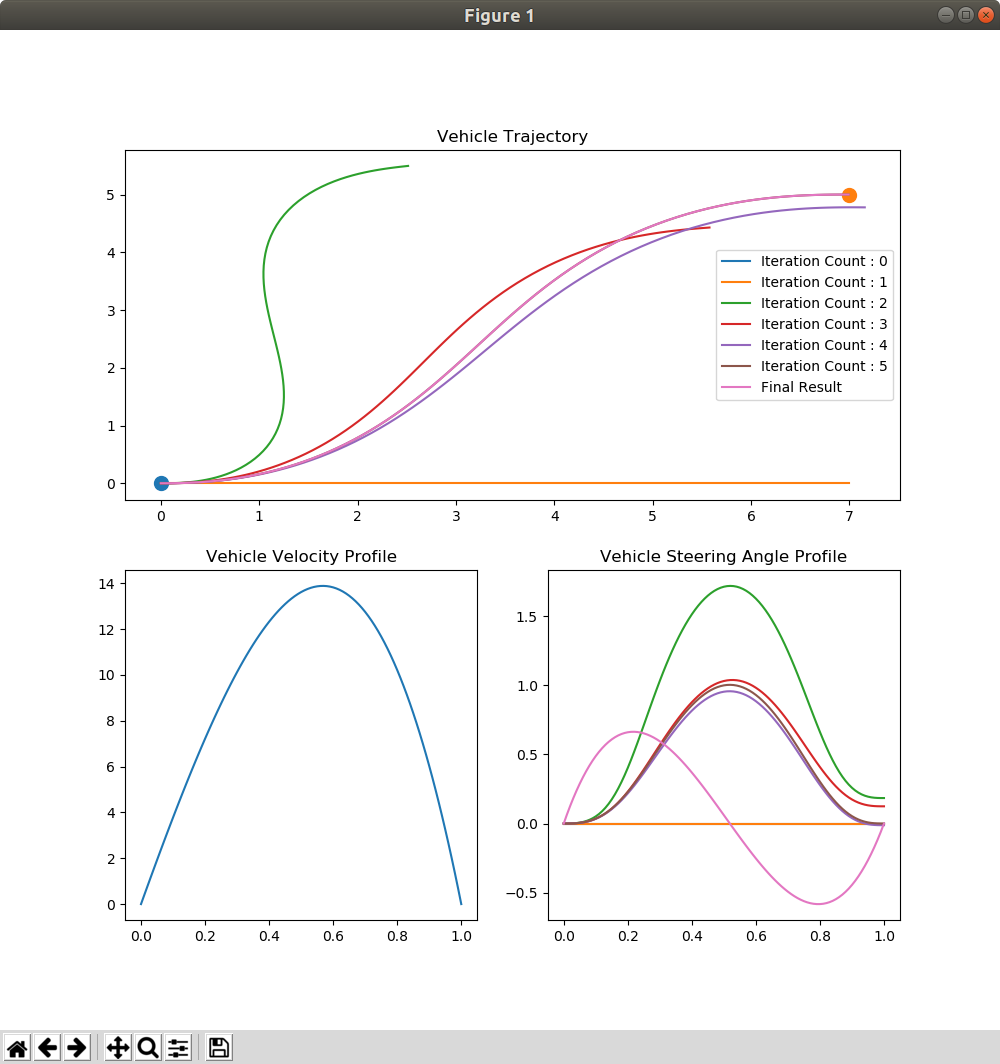
X.実験2(収束しない場合)
実験1はいい感じに目標に対して収束していきました.「じゃあ,収束しないときはどうなんの?」という疑問が湧いたので,実験してみます.上の結果を見てわかるとおり,レーンチェンジのマヌーバーはハンドルを左右に切らないと行けないので二次式では表現できません.ここではあえて,速度,ステアリング角を2次式でモデル化して問題を解いてみます.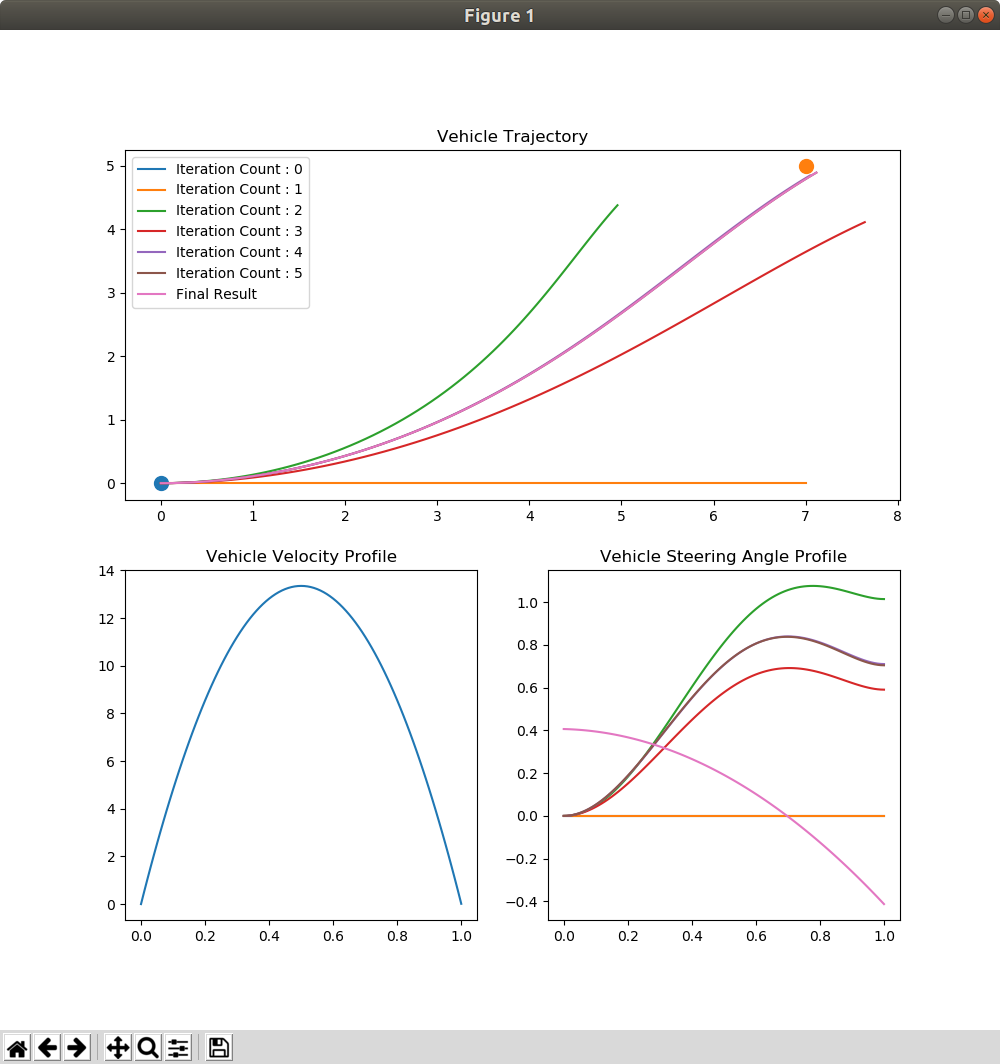
上図を見るとわかると思うのですが,目標に対して収束しませんでした.また,開始端,終了端ともに境界条件を満たせておらず,下記のような誤差になりました.
[dx_st, dy_st, dφ_st, dv_st, dθ_st, dx_end, dy_end, dφ_end, dv_end, dθ_end]
=
[ 0, 0, 0, -8.7e-05, -4.1e-01, -1.1e-01, 1.0e-01 -7.0e-01, -1.2e-02, 4.1e-01]
ということで,実際にこのアルゴリズムを使うときは
1.収束に必要であろう回数を定義して,最適化計算を実施.
X.実験で使ったコード
Planner の学習過程で作ったサンプルコードはここに入れて行こうと思います.
github.com
X.参考文献
論文
Optimal rough terrain trajectory generation for wheeled mobile robots


