Scale Space

ということで，下記２つのエントリを経てやっとこさ Scale Space のとこまで来ました．
daily-tech.hatenablog.com
daily-tech.hatenablog.com
で， 微分フィルタ及び二階微分フィルタ（Laplacian Filter）のエントリの最後で，
「スケールが 2σ 位の被写体が写っている画像に対して，標準偏差が σ のガウスフィルタと二階微分フィルタを適用すると，被写体の部分が強く反応する．」
という話をしました．このエントリではこれを実際に実験＆確認して，最後に Scale Space の定義を紹介します．

Laplacian of Gaussian Filter を適用してみる．

ここでは，実験用に下記の画像を使います．

実験用のひまわり畑写真

この画像に写っているひまわりですが，大体下記のようなサイズ感になっています．

ひまわり畑写真 with サイズ円

ここで，赤の円が半径 45pix，青の円が半径 10pix，緑の円が半径 5pix になります．ちなみに，ひまわりは花の部分が黄色，種の部分が黒なので，円で囲ってある部分のエッジはx方向からスキャンしていくと，
「下がりエッジー＞上がりエッジ」
になります．なので，二階微分は
「下がりエッジー＞上がりエッジと上がりエッジー＞下がりエッジ」
の組み合わせになるので，「強く反応する＝円の中心付近で出力値が大きくなる」ことを意味します．

それではこの写真に対して，前回のエントリで実験した 「Laplacian of Gaussian Filter」を適用して結果を見てみます．理論的にはガウシアンフィルタの標準偏差が10pix くらいになったとこで青の円が強く反応（＝明るくなって）して，45pix くらいになったとこで赤の円が強く反応（＝明るくなって）するはずですが，，，実験してみます．

σ = 1.6

σ = 2.2

σ = 3.2

σ = 4.5

σ = 6.4

σ = 9.0（青の円付近のひまわりが強く反応．）

σ = 12.8

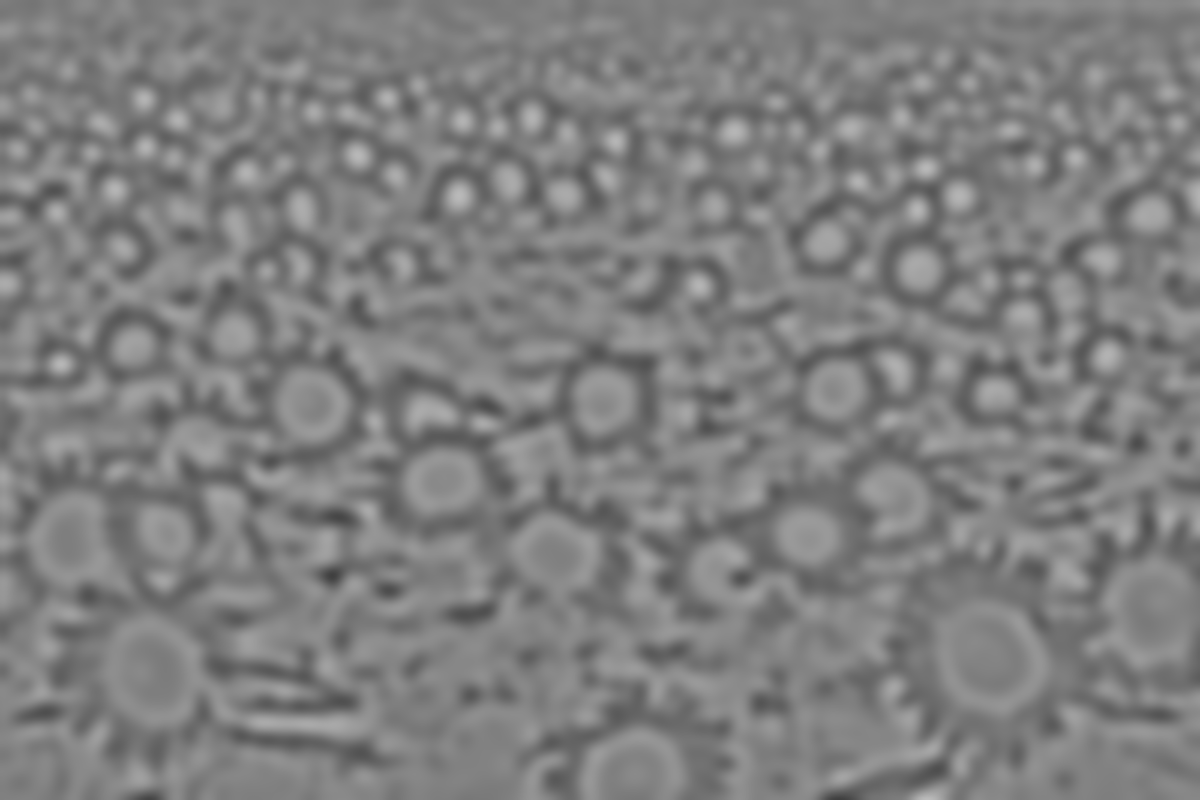
σ = 18.1

σ = 25.6（赤の円付近のひまわりが強く反応．）

σ = 36.2（赤の円付近のひまわりが強く反応．）

σ = 51.2

σ = 72.4

ちょっと写真でいっぱいになってしまいましたが，σが大きくなるにつれて強調されるひまわりが画像遠方から近方に写ってくる様子がわかると思います．遠方はほぼ黄色（花びらの部分）と茶色（種の部分）で構成されているのに対し，近方になってくると緑色（葉や茎）の要素が出てくるため，これによってエッジ構造が複雑になり，強め合い・弱め合いが起こることによって実際のサイズとピークを取るσからの乖離が大きくなってしまいました．が，ある程度は理論に沿った動きをすることがわかりました．

Scale Spaceの定義．

上記ひまわり畑の実験を踏まえると，LoG Filter (Laplacian of Gaussian Filter) のσを変化させることで，スケールが大体 σ 位の物体・構造を検知することができるようになりました．そこで，画像の縦・横に加え，新たにσの次元を加えることによって，画像中にどんなスケールの物体が写っているかがある程度わかるようになります．下記，簡単ですがいつものポンチ絵です．

Scale Space のイメージ

図中にスケールがそれぞれ r1, r2, r3 である３つの物体が書かれていますが，σ を変化させて LoG filter をかけ，その反応が強くなった箇所を書き留めておくことによって，書き留めた座標 (x, y) を中心とする物体のスケールが大体 σ くらいであるということがわかるようになります．SIFTではこの原理を使って特徴点を抽出します．ということで，次は SIFT に入ります．あー．時間がかかる．．．

実験に使ったコード．

github.com

import os
import cv2
import numpy as np


def scale_space_test1():

    cur_dir = os.path.dirname(os.path.abspath(__file__))
    path = cur_dir + '/../data/himawari.jpg'
    img = cv2.imread(path)
    gray_img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)

    k = np.sqrt(2)
    sigma = 1.6

    # for sigma in sigmas:
    for i in range(12):
        sigma_3_radius = 10 * sigma * 2

        # Applying Gaussian filter
        gauss_kernel_1d = cv2.getGaussianKernel(
            ksize=int(sigma_3_radius), sigma=sigma)
        gauss_kernel_2d = np.outer(
            gauss_kernel_1d, gauss_kernel_1d.transpose())
        log_filter = cv2.Laplacian(gauss_kernel_2d, cv2.CV_32FC1, ksize=31)

        laplacian_of_gaussian = cv2.filter2D(
            gray_img, cv2.CV_32FC1, log_filter)

        # Normalize value for visualization.
        min_val, max_val, _, _ = cv2.minMaxLoc(laplacian_of_gaussian)
        abs_max = max(abs(min_val), abs(max_val))
        tmp = (laplacian_of_gaussian * (0.5 / (2.0 * abs_max)) + 0.5) * 255.0
        laplacian_of_gaussian_uchar = np.uint8(tmp)

        title = 'Sigma = ' + str(sigma)
        cv2.namedWindow(title)
        cv2.imshow(title, laplacian_of_gaussian_uchar)
        #cv2.imwrite(title + str('.png'), laplacian_of_gaussian_uchar)
        cv2.waitKey(0)
        cv2.destroyWindow(title)

        sigma = k * sigma


if __name__ == "__main__":

    scale_space_test1()

参考文献．

Scale-space theory: A basic tool for analyzing structures at different scales

Distinctive image features from scale-invariant keypoints

http://www.cs.unc.edu/~lazebnik/spring11/lec08_blob.pdf