3.バンドル調整 ~ Sympy を使った微分計算
前回のエントリで回転のパラメータ化をしたことによって,透視投影の式から冗長なパラメータがなくなりました.ここからはバンドル調整を「制約のない最適化問題(Unconstrained Optimziation)」として解いていきます.
実際には3次元復元自体に "基準座標の不定性" と "スケールの不定性" があるので,まだ冗長性が残っているのですが,これは後のエントリで出てきます.
制約条件の無い最適化(Unconstrained Optimization)
最適化の方法をざっくりとおさらいしておきたいと思います.前提となるアイデアは,
「最急降下方向に下っていけばいつかは最小値にたどり着く.」
ですが,これをストレートに実施する方法が最急降下法で,もう少し工夫して収束を速めた方法がニュートン法ということになります.ここで,実際に最急降下法とニュートン法の更新ステップをみて,必要な微分式を洗い出しておきたいと思います.
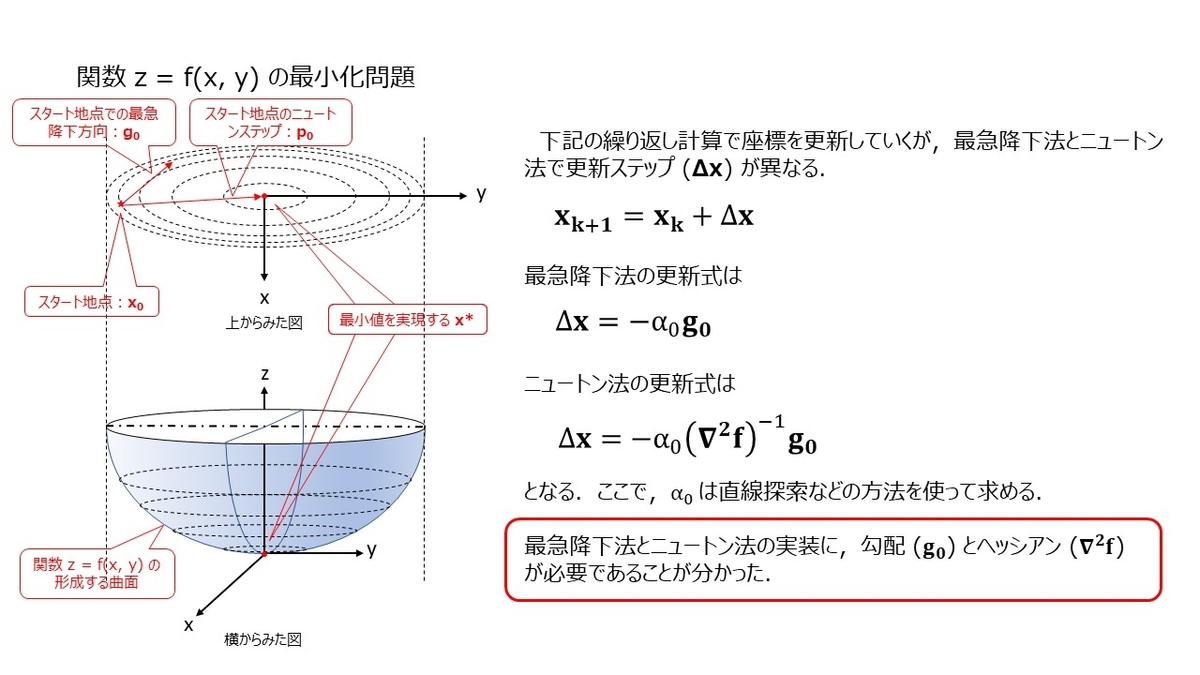

上記のスライドを見て頂ければわかる通り,変数の数が大きくなるとヘッシアンが巨大になります...次に,今回の問題の場合に勾配ベクトル,ヘッシアンがどうなるか見てみたいと思います.
バンドル調整の評価関数と微分
まず,今回の評価関数を再確認します.

この関数を微分していくことになります.シグマの形では見づらいので,ベクトルの Inner Product の形に式を変形しています.
Gradient,Hessianに出てくる微分要素
次に,実際に評価関数 E を任意のパラメータ x で微分したときにどうなるか見てみます.最終的に,勾配ベクトルはすべてのパラメータで E を偏微分したものをベクトルの形に並べたものになります.

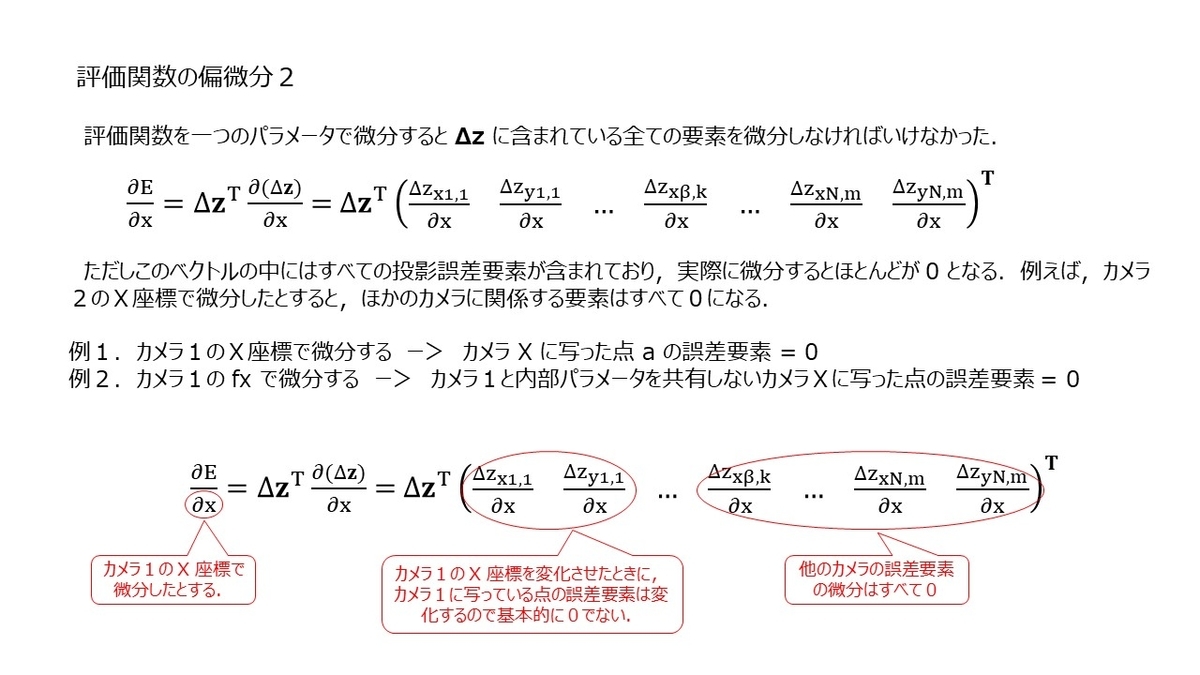


Sympy を使った微分計算
勾配ベクトルに必要な微分式は28個,ヘッシアンに必要な微分式は392個になりました.が,,,これを手計算するのはさすがにつらいので,ありがたく Sympy を使わせてもらいます.まず,Sympy による微分の方法ですが,とても簡単です.例として, f(x,y) = x*sin(x*x) + y*cos(y*y) を x と y に関して偏微分してみます.
import sympy if __name__ == "__main__": x = sympy.Symbol('x') y = sympy.Symbol('y') f = x * sympy.sin(x**2) + y * sympy.cos(y**2) print('df_dx : ' + str(sympy.diff(f, x))) print('df_dy : ' + str(sympy.diff(f, y)))
で,上記のコードを実行すると次のような結果が出ます.
df_dx : 2*x**2*cos(x**2) + sin(x**2) df_dy : -2*y**2*sin(y**2) + cos(y**2)
が,今回の実装では Python でなく C++ を使っているので,二乗の計算が "**2" になってしまうとつらいです....最初は置き換えしようとしてたんですがあまりの数の多さにげんなりしまして(笑)Cのフォーマットでプリントしてくれる方法を見つけました.
import sympy from sympy import ccode if __name__ == "__main__": x = sympy.Symbol('x') y = sympy.Symbol('y') f = x * sympy.sin(x**2) + y * sympy.cos(y**2) print('df_dx : ' + str(ccode(sympy.diff(f, x), standard='c89'))) print('df_dy : ' + str(ccode(sympy.diff(f, y), standard='c89')))
上記のコードを走らせると,,,,だだーん(゚Д゚)ノ
df_dx : 2*pow(x, 2)*cos(pow(x, 2)) + sin(pow(x, 2)) df_dy : -2*pow(y, 2)*sin(pow(y, 2)) + cos(pow(y, 2))
めでたしめでたし!です.
Sympy に微分させる実際の式
ということで,必要な微分式は上のスライドで導出したので,あとは Sympy に頑張ってもらえばよいだけです!本当に,ここまで立式した数式をそのまま突っ込んで実行すると計算してくれます.ありがたや...
ただ,回転のパラメータ化のところで触れたと思うのですが, Angle-Axis Representation では回転角が 0 のケースが特異点になります.この特異点を避けなければいけないので,角度の値に応じて数式を2種類用意します.
Symbolの定義.
# 1. 3D Point Coordinate. self.X = sympy.Symbol('p(0)') self.Y = sympy.Symbol('p(1)') self.Z = sympy.Symbol('p(2)') # 2. Internal Camera Parameters. self.fx = sympy.Symbol('K(0,0)') self.fy = sympy.Symbol('K(1,1)') self.cx = sympy.Symbol('K(0,2)') self.cy = sympy.Symbol('K(1,2)') self.s = sympy.Symbol('K(0,1)') self.f0 = sympy.Symbol('K(2,2)') self.K = sympy.Matrix([[self.fx, self.s, self.cx], [0, self.fy, self.cy], [0, 0, self.f0]]) # 3. External Camera Parameters. # Translation. self.tx = sympy.Symbol('T(0)') self.ty = sympy.Symbol('T(1)') self.tz = sympy.Symbol('T(2)') self.T = sympy.Matrix([self.tx, self.ty, self.tz]) # Rotation. self.vx = sympy.Symbol('rot(0)') self.vy = sympy.Symbol('rot(1)') self.vz = sympy.Symbol('rot(2)') self.theta = sympy.sqrt(self.vx**2 + self.vy**2 + self.vz**2) # Identity self.I = sympy.Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) # Outer product matrix self.W = sympy.Matrix([[0, -self.vz, self.vy], [self.vz, 0, -self.vx], [-self.vy, self.vx, 0]])
回転角度が一定以上あるとき.
self.R = self.I + (sympy.sin(self.theta) / self.theta) * self.W + \ ((1 - sympy.cos(self.theta)) / self.theta**2) * self.W * self.W self.P = self.K * (self.R.row_join(self.T)) self.x = self.P * sympy.Matrix([self.X, self.Y, self.Z, 1]) self.u = self.x[0] / self.x[2] self.v = self.x[1] / self.x[2]
回転角度が微小な時.
self.R = self.I + self.W
self.P = self.K * (self.R.row_join(self.T))
self.x = self.P * sympy.Matrix([self.X, self.Y, self.Z, 1])
self.u = self.x[0] / self.x[2]
self.v = self.x[1] / self.x[2]
で,上記コードの "self.u" が xpred, "self.y" が ypred になります.あとはこれを各要素で偏微分していけば微分要素がすべて出てきます.
実験コード
下記リポジトリの,blog_bundle_adjust/python/compute_derivatives_1st.py を実行すれば1階微分,blog_bundle_adjust/python/compute_derivatives_2nd.py を実行すれば2階微分が出力されます.
数が多いので,全部関数の形でターミナルにプリントアウトしています.それをコピペすれば,include だけ自分で書けばコンパイルが通るようなっています.なので,実際に実行すると下記の様な形で関数が出力されます.
(すみません.ファイルが出力されて,コンパイルすればそのままOK!にはなってません(笑))
inline double du2_dXdX(const Eigen::Vector3d &T, const Eigen::Vector3d &rot, const Eigen::Matrix3d &K, const Eigen::Vector3d &p, const Eigen::Vector3d &x) { double theta = std::pow( std::pow(rot(0), 2) + std::pow(rot(1), 2) + std::pow(rot(2), 2), 0.5); if (std::numeric_limits<double>::epsilon() < rot.dot(rot)) { return "回転角度が一定以上ある場合の微分式"; } else { return "回転角度が微小な場合の微分式"; } }
目次のページ
バンドル調整はシリーズ物として書いてまして,目次は下記のページになります.
daily-tech.hatenablog.com