謹賀新年２０２２！
５万人の読者の皆様！いかがお過ごしでしょうか？
大分遅くなってしまいましたが（笑），あけましておめでとうございます！
社長は変わらず元気にやってます(ﾟДﾟ)ﾉ
昨年はゴールデンウィークからずっとブログ更新できてなかったのですが，有難くも「ブログ更新してないじゃないですか(・´з`・)」と言ってもらったので，アップすることにしました！ただ，しばらく書いてないと何を書いていいかわからなくなりますね．．．ということで，ぎこちないですがお許しをm(__)m
２０２１年度ですが，実はいろいろとありまして，なかなか忙しくも充実した時間を過ごしてました！
【２０２１年のモロモロ】
１．１人オフィスの近くに引っ越し．（流山市ー＞船橋市）
もうだいぶたちましたが，引っ越しました！南流山に別れをつげて，やってきました船橋市．
２．つくばチャレンジのスポンサーになる．＆ 会社のロゴ作成
なりました！最後の写真をご覧あれ（笑）
３．つくばチャレンジ完走．
ロボット的には本当にあとちょっとのとこまで来ました！２０２２こそは完走を！
４．お客さん＆売上を増やす！
お客さんに恵まれたこともあって，運よくチャレンジできることになりました．ということで，絶賛仕事マラソン実施中です！本当に仕事一色の生活を送っています（笑）
やりたいことリスト！
今年のやりたいことリスト！ですが，期限を切らずにやっているので，結局昨年のアイテムをほぼそのまま持ってきた感じになっています（笑）想定以上に仕事中心の生活になっているので，勉強ネタがほとんど進まないですが，，，今年も（有難くも）仕事中心になりそうです．
【仕事ネタ】
１．海外から仕事をとってくる！
ここ２～３年のスパンで一つの目標にできればと思っています！ただ，税務とか法律とかが全く分からないので，ひとまず宣言だけ（笑）
【勉強ネタ】
１．つくばチャレンジのスポンサーになる．
引き続きスポンサーになります！
２．つくばチャレンジ完走．
今年こそは完走します！（笑）
３．ブログのリライト．
昔のエントリを見ていると結構嘘くさい（笑）ことを書いているので，復習もかねてリライトしたい！
４．SFMをやりきる．
うーん．散発的にしかできてない．．．．
５．ディープラーニングを勉強する．
うーん．やりたい．が，始められない．
６．数学力強化！
うーん．散発的にしかできてない．．．．
７．年に４本のブログアップ
うーん．ブログのアップが思った以上に進まず．．．あまり欲張らずに四半期に一度アップを目指します．
２０２２年！
ということで，今年もいままで通り，
All life is an experiment. The more experiments you make the better.
Ralph Waldo Emerson
をモットーに，いろんな実験をしていけたらと思います！ではでは，今年もよろしくお願いします！
うたの日コンサート
沖縄に，，，，行きたい行きたい行きた～い．
ということで沖縄病を発症してまして，ＢＥＧＩＮと夏川りみばっかり聞いてます（笑）
２年くらい前のアナザースカイにＢＥＧＩＮが出演してたんですが，２００１年から沖縄慰霊の日の翌日を歌の日として，「うたの日コンサート」というのを毎年開催しているみたいです．調べたところ結構有名なコンサートみたいで，一度行ってみたいと思っているのですが，昨年はコロナでオンラインになってしまい．．．今年こそは！と思ってひそかに予定をたててたんですが，どうやら延期になってしまったようです．．．
ただ，中止ではないみたいなので，タイミングが合えば行ってみたいなあ．
５．バンドル調整 〜 直線探索
ここでは，最適化に必要となる直線探索を扱います．これが，，，，なかなかに込み入ってて，とっても面倒でした．ただ，Numerical Optimization で紹介されているアルゴリズムの多くが直線探索に依存していたので，，，思い切って突っ込んで調べてみることにしました．簡単に実装はしてみたのですが，処理の流れを追う程度で見て頂ければと思います．実際に直線探索を作る必要がある方は， Ceres Solver とかを参考にしてみてください．
直線探索が必要になるとき
最急降下法を用いた時の収束の様子をイメージした図が下記になります．
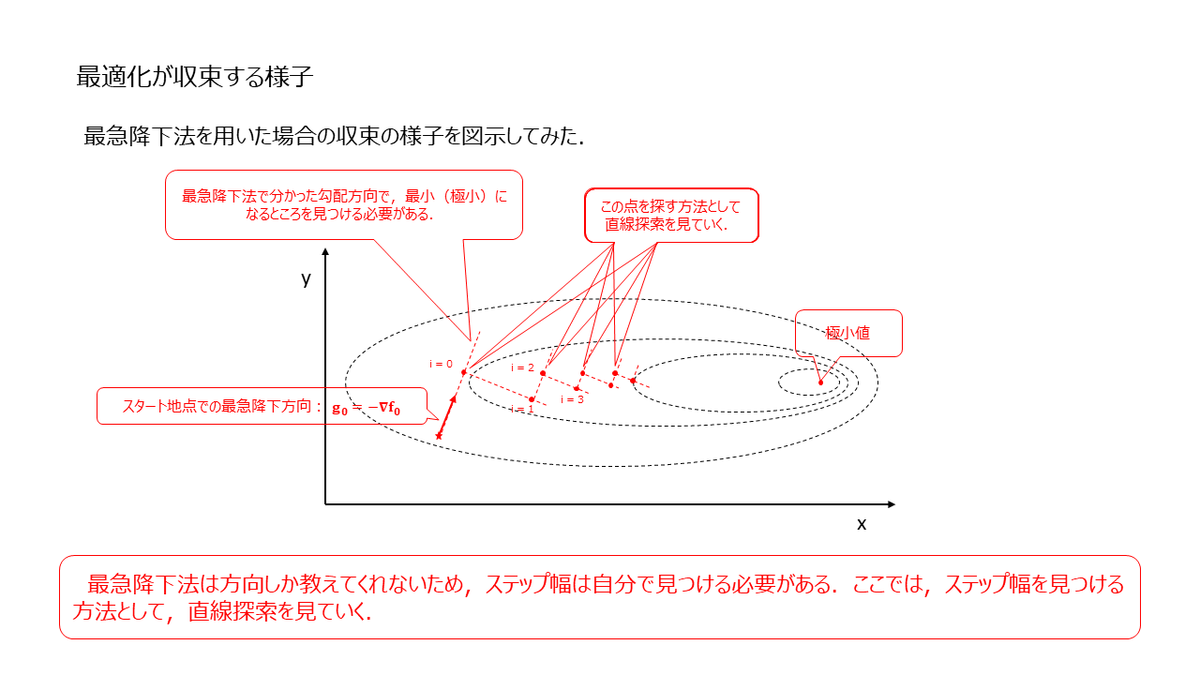
図からもわかるように，上手くいけば反復毎に最適値へと近づいていくことになります．ここで，方向（ステップ方向）は計算式によって与えられるものの，その方向にどれだけ進めばよいか（ステップ幅）は明示的に与えられないため，実験的に確かめて決めていく必要があります．これを実現する方法を直線探索と言って，関数の値が "前提条件" を満たすまで，所定の方向に沿っていろんなステップを試します．
次に，先ほど言及した "前提条件" ですが，この前提によって直線探索は "Exact Line Search" と "Inexact Line Search" にわかれます．
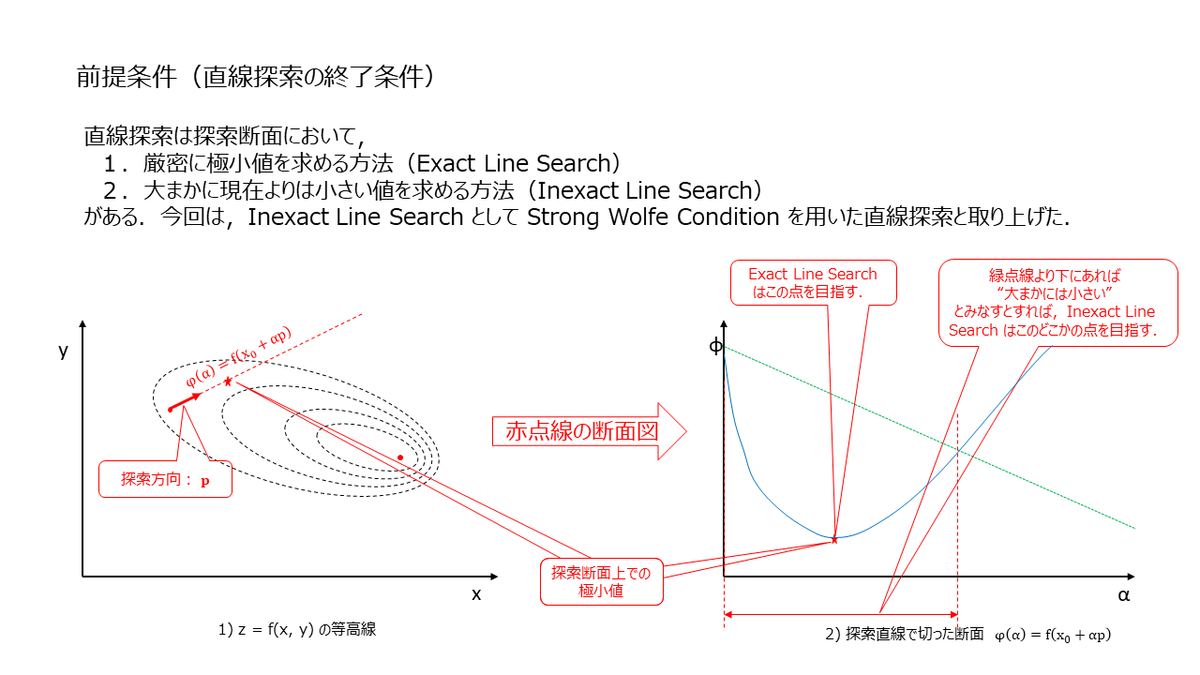
Exact Line Search はステップ方向に沿って厳密に極小値を求めていくため，必然的に実行時間が長くなります．ただ，実際には毎ステップ厳密に極小値を求めなくても最適値にはたどりつくようで，多くの最適化ソフトウェアでは Inexact Line Search が使われているようです．今回は，Numerical Optimization と Ceres Solver を参考に勉強したので，"前提条件" として Strong Wolfe Condition を使った直線探索を見ていきたいと思います．
Strong Wolfe Condition
Strong Wolfe Condition は下記の条件になります．
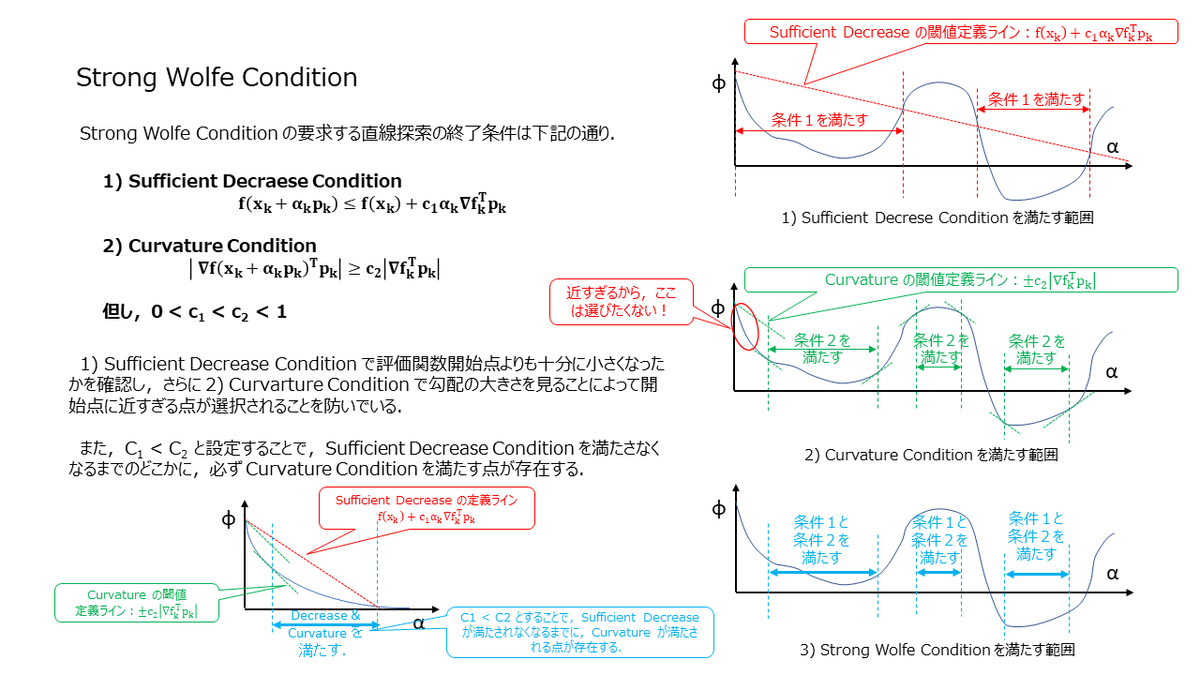
スライドにも記載のある通り，Curvature Condition を設定することによって，開始点に近すぎる点が次の計算点として選択されることを防いでいます．
Strong Wolfe を実装した直線探索法
これが思った以上にめんどくさく，とっても時間がかかったんですが（笑），スライドに挙動を起こしてみました．
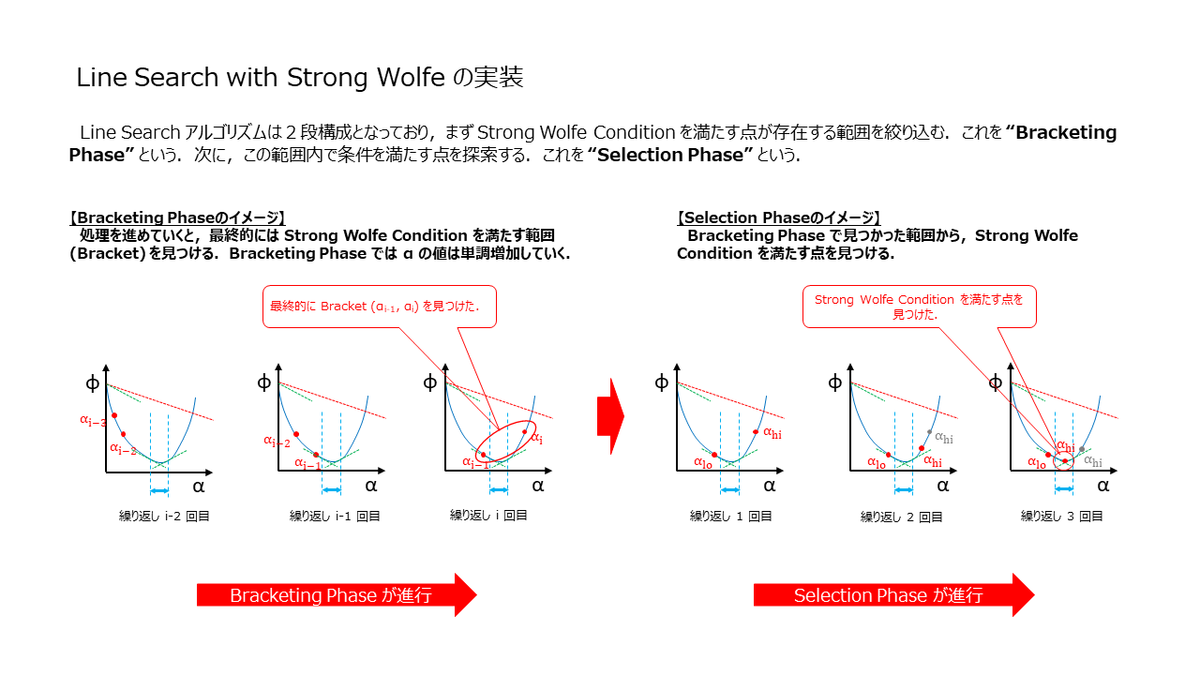
直線探索の実装は，Bracketing Phase と Selection Phase という２つの Phase に分かれます．まず，Bracketing Phase が走り，次に Selection Phase が走るのですが，それぞれの Phase でやっていることは，下記の様になります．
Bracketing Phase : Strong Wolfe Condition を満たすであろう点の存在する範囲（上記スライドの水色範囲）を探索する．
Selection Phase : Bracekting Phase で挟み込んだ範囲から，Strong Wolfe Condition を満たす点を探し出す．
となります．
Bracketing Phase の実装
ここでは，Bracketing Phase の実装を見ていきます．この Phase では範囲の絞り込みをやっています．いくつかケースを書き出して，図にしてみました．あと，実際にこのアルゴリズムを走らせる場合は数値計算的な部分（有限精度）も考慮する必要がありまして，範囲が狭くなりすぎるとループから抜けられなくなります．Bracket Size Check とスライドに記載した部分が該当の箇所になります．
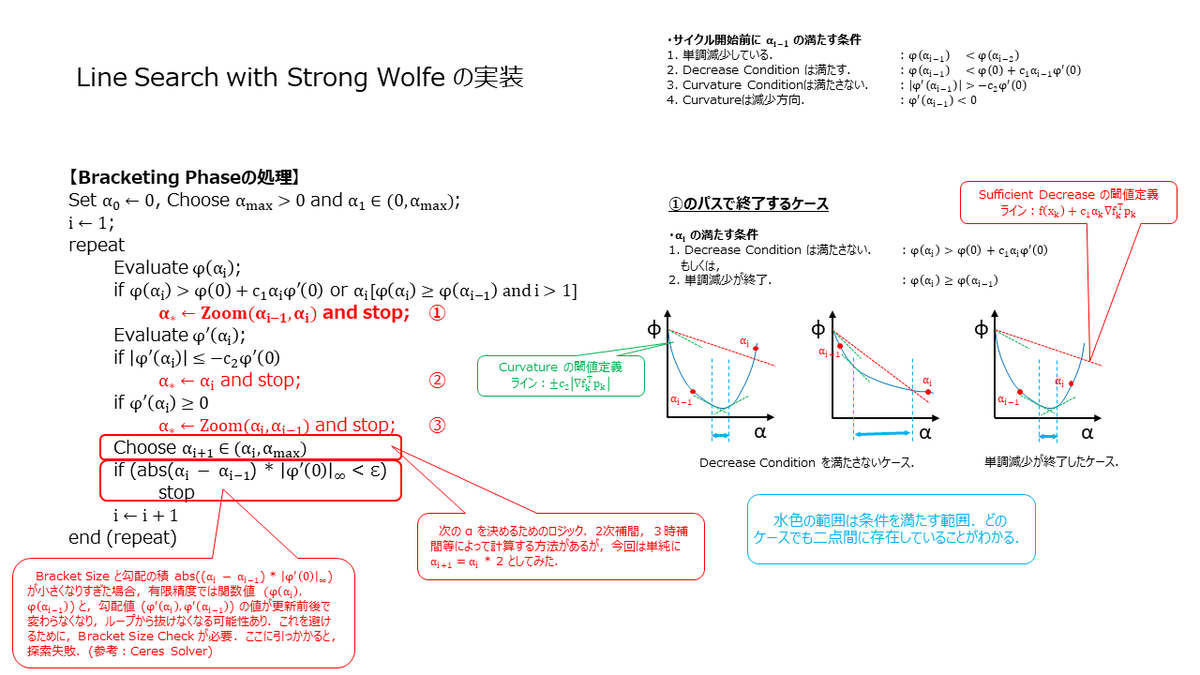
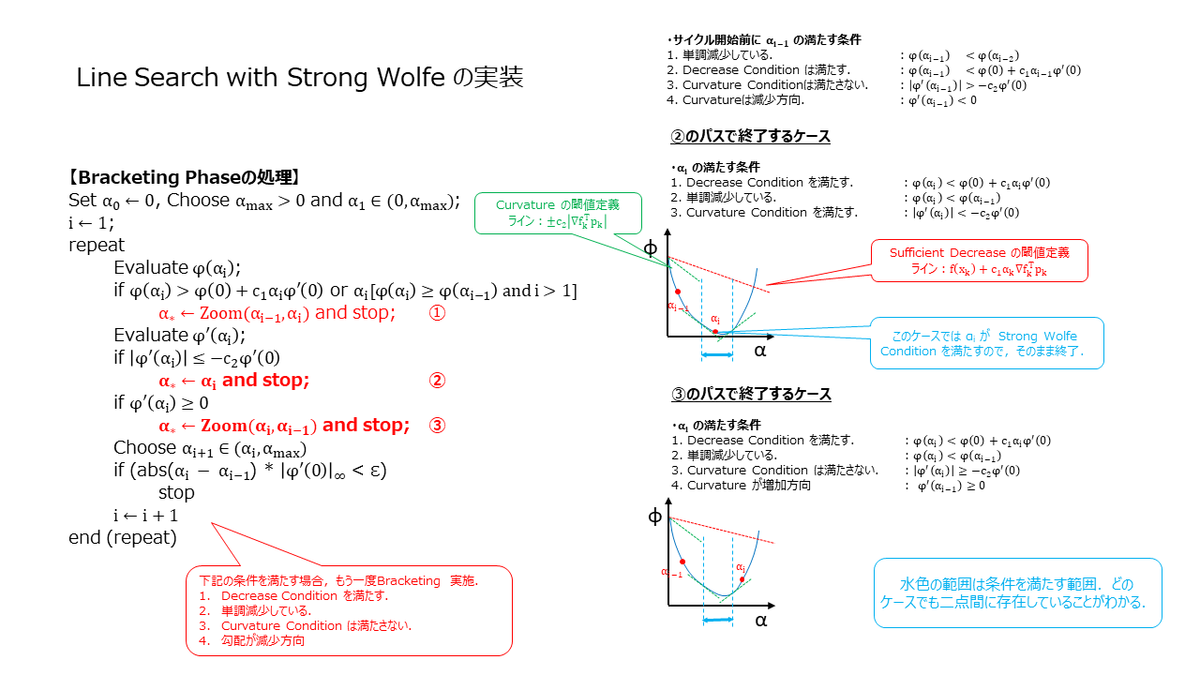
bool LineSearchWithStrongWolfe( const std::vector<Track>& tracks_src, const std::vector<Eigen::Matrix3d>& K_src, const std::vector<Eigen::Vector3d>& T_src, const std::vector<Eigen::Vector3d>& Rot_src, const std::vector<Eigen::Vector3d>& points3d_src, const std::map<size_t, size_t>& extrinsic_intrinsic_map, size_t max_itr, double min_step, double alpha_max, double c1, double c2, double& alpha_star) { // X. Temporary buffer. std::vector<Eigen::Vector3d> T_tmp = T_src; std::vector<Eigen::Matrix3d> K_tmp = K_src; std::vector<Eigen::Vector3d> Rot_tmp = Rot_src; std::vector<Eigen::Vector3d> points3d_tmp = points3d_src; // X. Compute base value & base gradient. double phi_0 = ComputeReprojectionError( tracks_src, K_tmp, extrinsic_intrinsic_map, Rot_tmp, T_tmp, points3d_tmp); Eigen::MatrixXd grad_0 = ComputeGradient(K_tmp, T_tmp, Rot_tmp, points3d_tmp, tracks_src, extrinsic_intrinsic_map); double grad_0_max_norm = grad_0.col(0).lpNorm<Eigen::Infinity>(); // X. Compute directional derivative. Eigen::MatrixXd step_dir = -grad_0.normalized(); double der_phi_0 = grad_0.col(0).dot(step_dir.col(0)); // X. Start iteration. double phi_i = phi_0; double phi_i_1 = phi_0; double der_phi_i = der_phi_0; double der_phi_i_1 = der_phi_0; // X. Initial alpha. double alpha_i_1 = 0; double alpha_i = std::min(1.0, alpha_max); // X. Status bool success = false; for (size_t itr = 0; itr < max_itr; itr++) { // X. Copy from original.. T_tmp = T_src; K_tmp = K_src; Rot_tmp = Rot_src; points3d_tmp = points3d_src; // X. Update parameters based on alpha. UpdateParameters(alpha_i * -grad_0, tracks_src, extrinsic_intrinsic_map, K_tmp, T_tmp, Rot_tmp, points3d_tmp); // X. Compute function value at alpha_i. phi_i = ComputeReprojectionError(tracks_src, K_tmp, extrinsic_intrinsic_map, Rot_tmp, T_tmp, points3d_tmp); // X. Condition 1. if (phi_i > phi_0 + c1 * alpha_i * der_phi_0 || (phi_i >= phi_i_1 && itr > 0)) { success = Zoom(tracks_src, K_src, T_src, Rot_src, points3d_src, extrinsic_intrinsic_map, alpha_i_1, alpha_i, c1, c2, max_itr, min_step, alpha_star); break; } // X. Compute gradient at alpha_i. Eigen::MatrixXd grad_i = ComputeGradient(K_tmp, T_tmp, Rot_tmp, points3d_tmp, tracks_src, extrinsic_intrinsic_map); der_phi_i = grad_i.col(0).dot(step_dir.col(0)); // X. Condition 2. if (std::abs(der_phi_i) <= -c2 * der_phi_0) { alpha_star = alpha_i; success = true; break; } // X. Condition 3. if (der_phi_i >= 0) { success = Zoom(tracks_src, K_src, T_src, Rot_src, points3d_src, extrinsic_intrinsic_map, alpha_i, alpha_i_1, c1, c2, max_itr, min_step, alpha_star); break; } // X. Bracket range can not be found. Retry with different alpha alpha_i_1 = alpha_i; alpha_i = std::min(2 * alpha_i, alpha_max); phi_i_1 = phi_i; der_phi_i_1 = der_phi_i; // X. Bracket Size Check if ((std::abs(alpha_i - alpha_i_1) * grad_0_max_norm < min_step) || (alpha_i_1 == alpha_max)) { success = false; alpha_star = alpha_i_1; break; } } return success; }
※この実装，数値計算的なところも考慮する必要があり，思った以上に込み入ってまして（笑）流れを理解するために見て頂ければと思います．確実な詳細を知りたい方は，Google 先生の下記のコードをご覧あれ．
ceres-solver/line_search.cc at master · ceres-solver/ceres-solver · GitHub
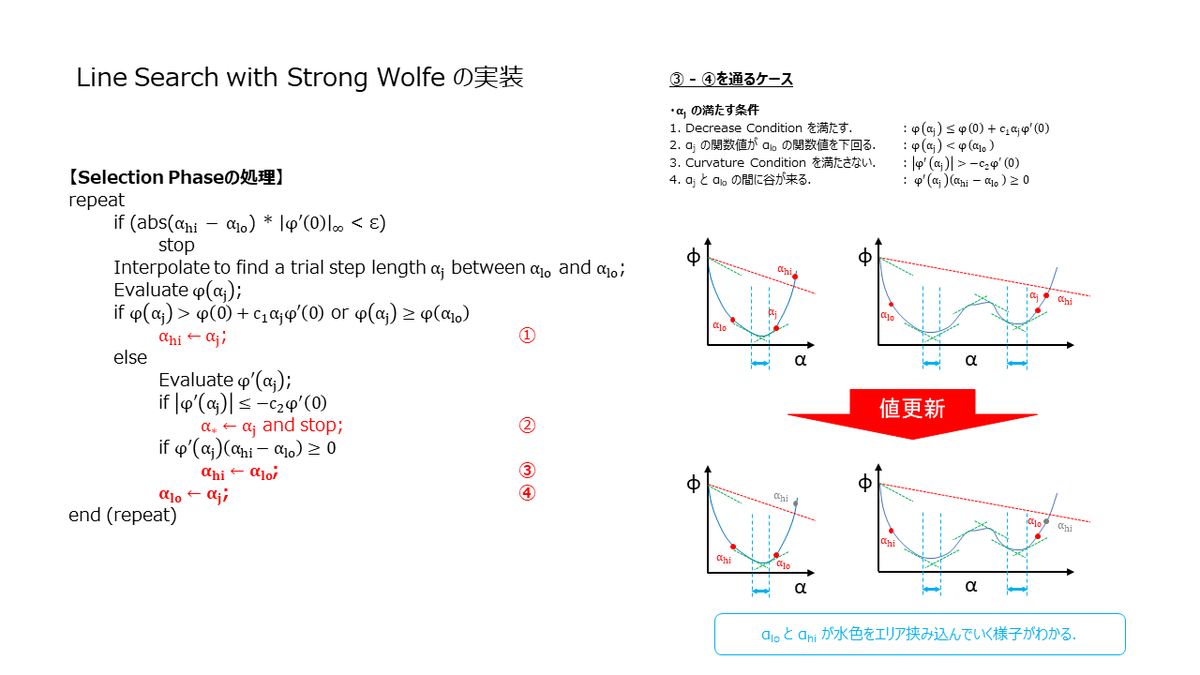
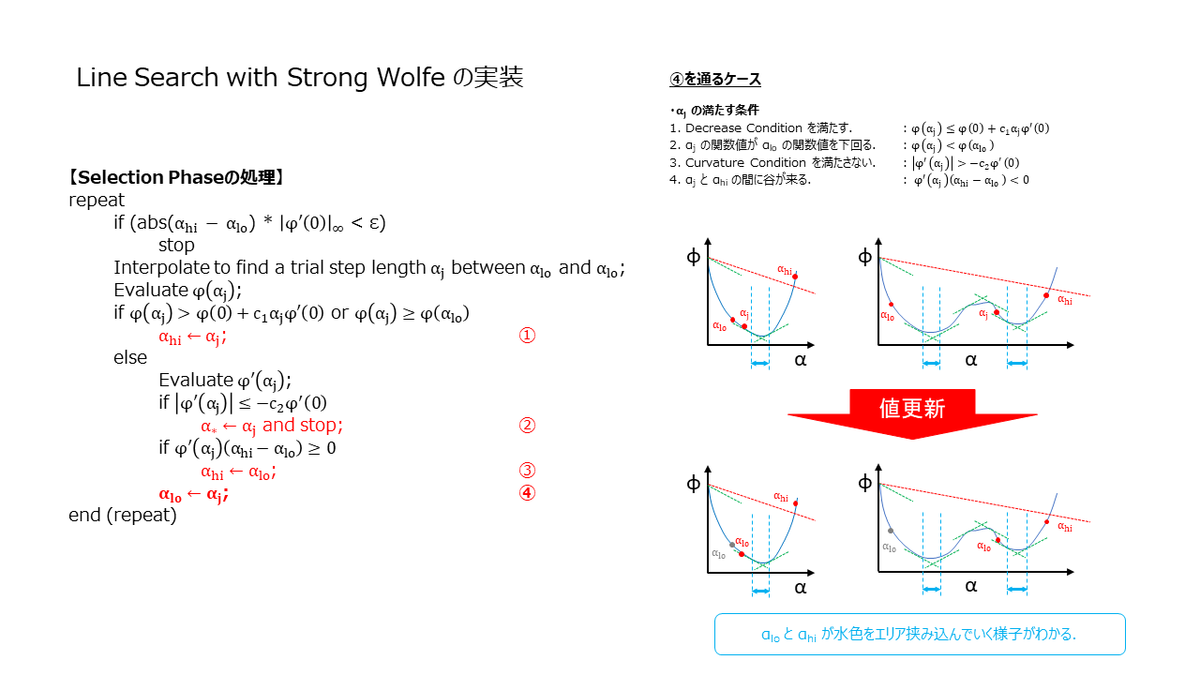
Selection Phase の実装
ここでは，Selection Phase の実装を見ていきます．Selection Phase は，Braceking Phase で Zoom(αi，αj) と記載した関数の実装になりますが，Zoom 関数に渡される時点で下記の前提が成立している必要があります．前提条件が満たされない場合，Strong Wolfe を満たす点が見つからない可能性があります．
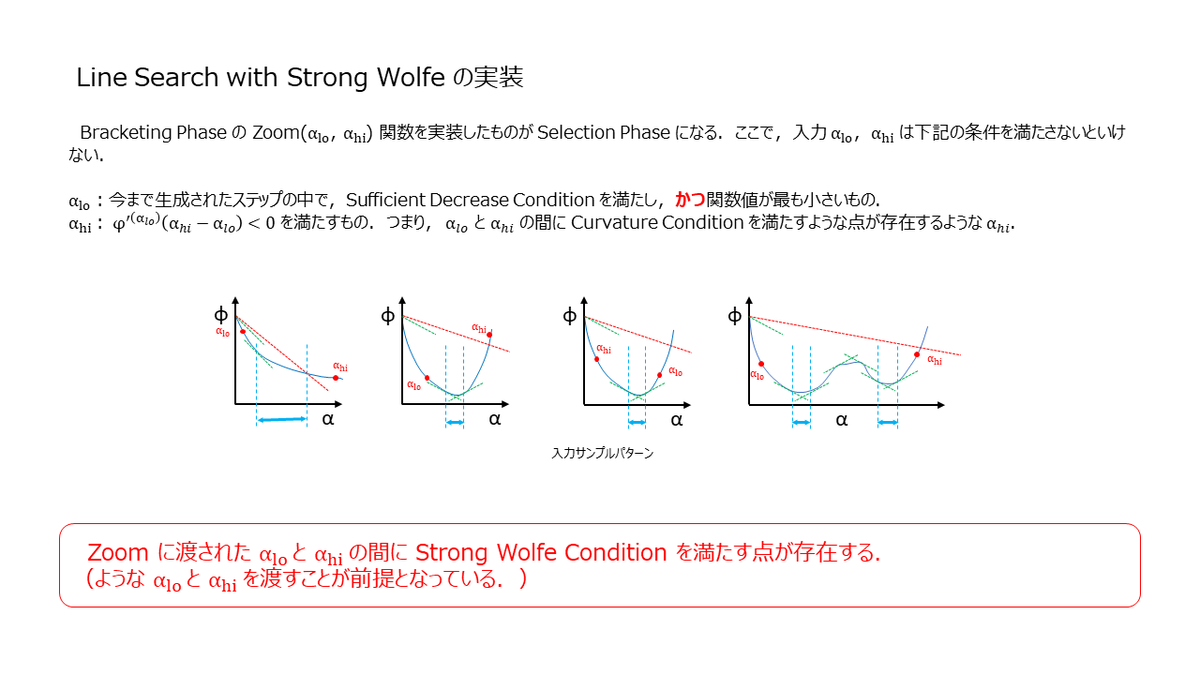
ここでも数値計算的な部分（有限精度）を考慮する必要がありまして，範囲が狭くなりすぎるとループから抜けられなくなります．Bracket Size Check とスライドに記載した部分が該当の箇所になります．また Selection Phase では，２次補間や３次補間を使って次の α を選択していましたが，今回は簡単のために中間点を使っています．
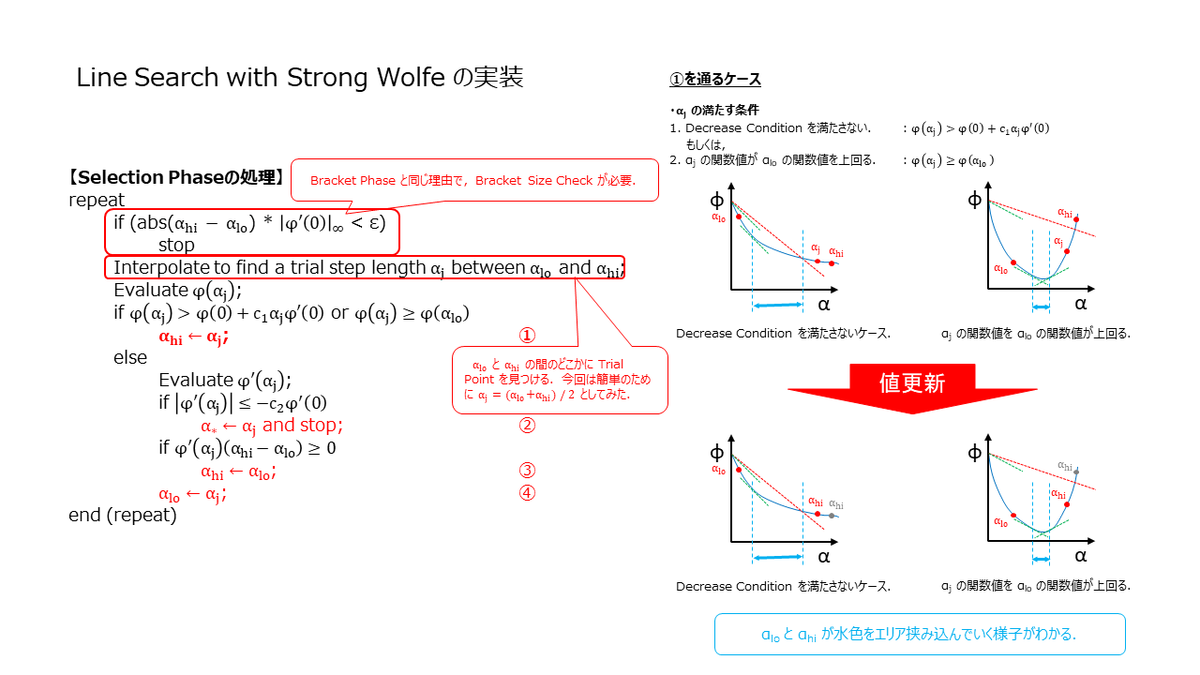
bool Zoom(const std::vector<Track>& tracks_src, const std::vector<Eigen::Matrix3d>& K_src, const std::vector<Eigen::Vector3d>& T_src, const std::vector<Eigen::Vector3d>& Rot_src, const std::vector<Eigen::Vector3d>& points3d_src, const std::map<size_t, size_t>& extrinsic_intrinsic_map, double alpha_low, double alpha_high, double c1, double c2, size_t max_itr, double min_step, double& alpha_star) { // X. Compute base value & base gradient. double phi_0 = ComputeReprojectionError( tracks_src, K_src, extrinsic_intrinsic_map, Rot_src, T_src, points3d_src); Eigen::MatrixXd grad_0 = ComputeGradient(K_src, T_src, Rot_src, points3d_src, tracks_src, extrinsic_intrinsic_map); double grad_0_max_norm = grad_0.col(0).lpNorm<Eigen::Infinity>(); // X. Compute directional derivative. Eigen::MatrixXd step_dir = -grad_0.normalized(); double der_phi_0 = grad_0.col(0).dot(step_dir.col(0)); // X. Compute value at alpha_low. double phi_lo = ComputeReprojectionErrorWithStepLength( -grad_0, alpha_low, tracks_src, K_src, T_src, Rot_src, points3d_src, extrinsic_intrinsic_map); // X. Initial alpha double alpha_low_tmp_ = alpha_low; double alpha_high_tmp_ = alpha_high; // X. Result bool success = false; for (size_t itr = 0; itr < max_itr; itr++) { // X. Bracket Size Check if ((std::abs(alpha_high_tmp_ - alpha_low_tmp_) * grad_0_max_norm < min_step)) { success = false; alpha_star = alpha_low; break; } // X. Find trial value. double alpha_j = ComputeTrialValues(alpha_low_tmp_, alpha_high_tmp_); // X. Update parameters based on alpha. std::vector<Eigen::Vector3d> T_tmp = T_src; std::vector<Eigen::Matrix3d> K_tmp = K_src; std::vector<Eigen::Vector3d> Rot_tmp = Rot_src; std::vector<Eigen::Vector3d> points3d_tmp = points3d_src; UpdateParameters(alpha_j * -grad_0, tracks_src, extrinsic_intrinsic_map, K_tmp, T_tmp, Rot_tmp, points3d_tmp); double phi_j = ComputeReprojectionError(tracks_src, K_tmp, extrinsic_intrinsic_map, Rot_tmp, T_tmp, points3d_tmp); if (phi_j > phi_0 + c1 * alpha_j * der_phi_0 || phi_j >= phi_lo) { // X. Shrink upper window. alpha_high_tmp_ = alpha_j; } else { // X. Evaluate derivative value. Eigen::MatrixXd grad_j = ComputeGradient(K_tmp, T_tmp, Rot_tmp, points3d_tmp, tracks_src, extrinsic_intrinsic_map); double der_phi_j = grad_j.col(0).dot(step_dir.col(0)); // X. Find point satisfying wolfe condition. if (std::abs(der_phi_j) <= -c2 * der_phi_0) { alpha_star = alpha_j; success = true; break; } // X. Shrink upper window. if (der_phi_j * (alpha_high_tmp_ - alpha_low_tmp_) >= 0) { alpha_high_tmp_ = alpha_low_tmp_; } // X. Shrink lower window. alpha_low_tmp_ = alpha_j; phi_lo = phi_j; } } return success; }
※この実装，数値計算的なところも考慮する必要があり，思った以上に込み入ってまして（笑）流れを理解するために見て頂ければと思います．確実な詳細を知りたい方は，Google 先生の下記のコードをご覧あれ．
ceres-solver/line_search.cc at master · ceres-solver/ceres-solver · GitHub
ふ～．ということで，次に行きます！
実験コード
目次のページ
バンドル調整はシリーズ物として書いてまして，目次は下記のページになります．
daily-tech.hatenablog.com
４．バンドル調整 〜 勾配ベクトルとヘッシアンの作成
このエントリでは，バンドル調整のヘッシアンが典型的にはどのような構造になるかを見てみます．その後，それに基づいて勾配ベクトルとヘッシアンを作ります．
ニュートン法からヘッシアンを考える．
上記の通り，とくに行列が大きくなってくると「エイや！」で計算してはいけないようです．ということで，今回の実験におけるヘッシアンがどのような構造になっているか見てみます．
勾配ベクトルとヘッシアンの構造
上記が今回のケースでのヘッシアンですが，右下のブロックに白のセルが目立つと思います．下のスライドで説明していますが，パラメータ間につながりがないもの同志で評価関数を微分すると０になるため，これが該当するヘッシアンのセルが０になっています．
例えば，下記のようなケースで二階微分がゼロになってます．
・評価関数を異なるカメラの外部パラメータで微分したもの．
・評価関数を異なる点で微分したもの．
・評価関数をあるカメラの外部パラメータで微分し，当該カメラと異なる内部パラメータで微分したもの．
次に，右下のブロックが Sparse であることを生かして，方程式を解いていきます．
シューアの補行列を使ってニュートンステップの計算
※ここでの議論では，ヘッシアンの正定性はすでに仮定してあります．
シューアの補行列を用いて，巨大な一つの線形方程式群を二つに分割できました．分割するだけだと計算量的にあまりメリットはないのかもしれませんが，ここで右下ブロックの Sparsity を使います．
勾配ベクトルの実装
ちなみに，実際の勾配ベクトルの計算は次の様になりました．ヘッシアンも同じような形で計算したのですが，多いので省きます（笑）
ヘッシアンの計算：
https://github.com/koichiHik/blog_bundle_adjust/blob/main/src/optimization/src/compute_hessian.cc
ヘッシアンに関しては，自分はメモリをすべて確保してから単純にそれぞれの要素を加えていったのですが，０の要素がいっぱいできてしまうのでこれは非効率で，本当は非ゼロの要素にだけメモリを割り当ててニュートンステップを計算するみたいです．
詳しくは下記の論文をどうぞ．．．
SBA: A software package for generic sparse bundle adjustment
勾配の計算部分を少しだけ．．．
// すべてのカメラでループ． for (size_t cam_ext_idx = 0; cam_ext_idx < cam_ext_num; cam_ext_idx++) { // すべての３次元点でループ． for (size_t trk_idx = 0; trk_idx < track_num; trk_idx++) { // 当該カメラに３次元点が写っていれば． if (tracks[trk_idx].count(cam_ext_idx)) { Eigen::Vector2d meas = tracks[trk_idx].at(cam_ext_idx); Eigen::Vector3d x = cameras[cam_ext_idx] * points3d[trk_idx].homogeneous(); Eigen::Vector2d proj = x.hnormalized(); // ０．残差の計算． double u_res = proj(0) - meas(0); double v_res = proj(1) - meas(1); // １．勾配のカメラ外部パラメータ部分の計算 size_t cam_int_idx = extrinsic_intrinsic_map.at(cam_ext_idx); { size_t col_idx = cam_ext_idx * cam_ext_var_num; grad(col_idx, 0) += u_res * du_dtx(T[cam_ext_idx], Rot[cam_ext_idx], K[cam_int_idx], points3d[trk_idx], x) + v_res * dv_dtx(T[cam_ext_idx], Rot[cam_ext_idx], K[cam_int_idx], points3d[trk_idx], x); // y, z, kx, ky, kz についても同様に計算 ・・・・・ } // ２．勾配のカメラ内部パラメータ部分の計算 { double scale = 1.0; size_t col_idx = cam_ext_num * cam_ext_var_num + cam_int_idx * cam_int_var_num; grad(col_idx, 0) += scale * (u_res * du_dfx(T[cam_ext_idx], Rot[cam_ext_idx], K[cam_int_idx], points3d[trk_idx], x) + v_res * dv_dfx(T[cam_ext_idx], Rot[cam_ext_idx], K[cam_int_idx], points3d[trk_idx], x)); // y, z, kx, ky, kz についても同様に計算 ・・・・・ } // ３．勾配の点群位置パラメータ部分の計算 { size_t col_idx = cam_ext_num * cam_ext_var_num + cam_int_num * cam_int_var_num + trk_idx * points_var_num; grad(col_idx, 0) += u_res * du_dX(T[cam_ext_idx], Rot[cam_ext_idx], K[cam_int_idx], points3d[trk_idx], x) + v_res * dv_dX(T[cam_ext_idx], Rot[cam_ext_idx], K[cam_int_idx], points3d[trk_idx], x); // Y，Z についても同様に計算 ・・・・・ } } } }
３．バンドル調整 ～ Sympy を使った微分計算
前回のエントリで回転のパラメータ化をしたことによって，透視投影の式から冗長なパラメータがなくなりました．ここからはバンドル調整を「制約のない最適化問題（Unconstrained Optimziation）」として解いていきます．
実際には３次元復元自体に "基準座標の不定性" と "スケールの不定性" があるので，まだ冗長性が残っているのですが，これは後のエントリで出てきます．
制約条件の無い最適化（Unconstrained Optimization）
最適化の方法をざっくりとおさらいしておきたいと思います．前提となるアイデアは，
「最急降下方向に下っていけばいつかは最小値にたどり着く．」
ですが，これをストレートに実施する方法が最急降下法で，もう少し工夫して収束を速めた方法がニュートン法ということになります．ここで，実際に最急降下法とニュートン法の更新ステップをみて，必要な微分式を洗い出しておきたいと思います．
上記のスライドを見て頂ければわかる通り，変数の数が大きくなるとヘッシアンが巨大になります．．．次に，今回の問題の場合に勾配ベクトル，ヘッシアンがどうなるか見てみたいと思います．
バンドル調整の評価関数と微分
まず，今回の評価関数を再確認します．
この関数を微分していくことになります．シグマの形では見づらいので，ベクトルの Inner Product の形に式を変形しています．
Gradient，Hessianに出てくる微分要素
次に，実際に評価関数 E を任意のパラメータ x で微分したときにどうなるか見てみます．最終的に，勾配ベクトルはすべてのパラメータで E を偏微分したものをベクトルの形に並べたものになります．
Sympy を使った微分計算
勾配ベクトルに必要な微分式は２８個，ヘッシアンに必要な微分式は３９２個になりました．が，，，これを手計算するのはさすがにつらいので，ありがたく Sympy を使わせてもらいます．まず，Sympy による微分の方法ですが，とても簡単です．例として， f(x,y) = x*sin(x*x) + y*cos(y*y) を x と y に関して偏微分してみます．
import sympy if __name__ == "__main__": x = sympy.Symbol('x') y = sympy.Symbol('y') f = x * sympy.sin(x**2) + y * sympy.cos(y**2) print('df_dx : ' + str(sympy.diff(f, x))) print('df_dy : ' + str(sympy.diff(f, y)))
で，上記のコードを実行すると次のような結果が出ます．
df_dx : 2*x**2*cos(x**2) + sin(x**2) df_dy : -2*y**2*sin(y**2) + cos(y**2)
が，今回の実装では Python でなく C++ を使っているので，二乗の計算が "**2" になってしまうとつらいです．．．．最初は置き換えしようとしてたんですがあまりの数の多さにげんなりしまして（笑）Cのフォーマットでプリントしてくれる方法を見つけました．
import sympy from sympy import ccode if __name__ == "__main__": x = sympy.Symbol('x') y = sympy.Symbol('y') f = x * sympy.sin(x**2) + y * sympy.cos(y**2) print('df_dx : ' + str(ccode(sympy.diff(f, x), standard='c89'))) print('df_dy : ' + str(ccode(sympy.diff(f, y), standard='c89')))
上記のコードを走らせると，，，，だだーん(ﾟДﾟ)ﾉ
df_dx : 2*pow(x, 2)*cos(pow(x, 2)) + sin(pow(x, 2)) df_dy : -2*pow(y, 2)*sin(pow(y, 2)) + cos(pow(y, 2))
めでたしめでたし！です．
Sympy に微分させる実際の式
ということで，必要な微分式は上のスライドで導出したので，あとは Sympy に頑張ってもらえばよいだけです！本当に，ここまで立式した数式をそのまま突っ込んで実行すると計算してくれます．ありがたや．．．
ただ，回転のパラメータ化のところで触れたと思うのですが， Angle-Axis Representation では回転角が 0 のケースが特異点になります．この特異点を避けなければいけないので，角度の値に応じて数式を２種類用意します．
Symbolの定義．
# 1. 3D Point Coordinate. self.X = sympy.Symbol('p(0)') self.Y = sympy.Symbol('p(1)') self.Z = sympy.Symbol('p(2)') # 2. Internal Camera Parameters. self.fx = sympy.Symbol('K(0,0)') self.fy = sympy.Symbol('K(1,1)') self.cx = sympy.Symbol('K(0,2)') self.cy = sympy.Symbol('K(1,2)') self.s = sympy.Symbol('K(0,1)') self.f0 = sympy.Symbol('K(2,2)') self.K = sympy.Matrix([[self.fx, self.s, self.cx], [0, self.fy, self.cy], [0, 0, self.f0]]) # 3. External Camera Parameters. # Translation. self.tx = sympy.Symbol('T(0)') self.ty = sympy.Symbol('T(1)') self.tz = sympy.Symbol('T(2)') self.T = sympy.Matrix([self.tx, self.ty, self.tz]) # Rotation. self.vx = sympy.Symbol('rot(0)') self.vy = sympy.Symbol('rot(1)') self.vz = sympy.Symbol('rot(2)') self.theta = sympy.sqrt(self.vx**2 + self.vy**2 + self.vz**2) # Identity self.I = sympy.Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]]) # Outer product matrix self.W = sympy.Matrix([[0, -self.vz, self.vy], [self.vz, 0, -self.vx], [-self.vy, self.vx, 0]])
回転角度が一定以上あるとき．
self.R = self.I + (sympy.sin(self.theta) / self.theta) * self.W + \ ((1 - sympy.cos(self.theta)) / self.theta**2) * self.W * self.W self.P = self.K * (self.R.row_join(self.T)) self.x = self.P * sympy.Matrix([self.X, self.Y, self.Z, 1]) self.u = self.x[0] / self.x[2] self.v = self.x[1] / self.x[2]
回転角度が微小な時．
self.R = self.I + self.W
self.P = self.K * (self.R.row_join(self.T))
self.x = self.P * sympy.Matrix([self.X, self.Y, self.Z, 1])
self.u = self.x[0] / self.x[2]
self.v = self.x[1] / self.x[2]
で，上記コードの "self.u" が xpred, "self.y" が ypred になります．あとはこれを各要素で偏微分していけば微分要素がすべて出てきます．
実験コード
下記リポジトリの，blog_bundle_adjust/python/compute_derivatives_1st.py を実行すれば１階微分，blog_bundle_adjust/python/compute_derivatives_2nd.py を実行すれば２階微分が出力されます．
数が多いので，全部関数の形でターミナルにプリントアウトしています．それをコピペすれば，include だけ自分で書けばコンパイルが通るようなっています．なので，実際に実行すると下記の様な形で関数が出力されます．
（すみません．ファイルが出力されて，コンパイルすればそのままOK！にはなってません（笑)）
inline double du2_dXdX(const Eigen::Vector3d &T, const Eigen::Vector3d &rot, const Eigen::Matrix3d &K, const Eigen::Vector3d &p, const Eigen::Vector3d &x) { double theta = std::pow( std::pow(rot(0), 2) + std::pow(rot(1), 2) + std::pow(rot(2), 2), 0.5); if (std::numeric_limits<double>::epsilon() < rot.dot(rot)) { return "回転角度が一定以上ある場合の微分式"; } else { return "回転角度が微小な場合の微分式"; } }
目次のページ
バンドル調整はシリーズ物として書いてまして，目次は下記のページになります．
daily-tech.hatenablog.com
２．バンドル調整 ～ 回転のパラメータ化
透視投影の式
前回エントリで扱ったモデル化で，カメラの透視投影の式を導出しました．下図のように基準座標となるカメラを決定すると，
カメラの投影点を求めるためには下記の式を使う必要がありました．
ここで，各変数の自由度は次のようになります．
- 各カメラの併進ベクトル Tk : 自由度３
- 各カメラの内部パラメータ行列 Kk : 自由度５
- 各カメラの併進ベクトル Rk : 自由度３
併進ベクトル，内部パラメータ行列に関しては，設定した変数の数がそのまま自由度となっています．一方で，回転行列は 3x3 行列で表現しているので，一見すると変数は９個あるように見えますが，回転の自由度は３なので冗長な表現となっていることがわかります．
回転のパラメータ化の必要性
冗長な表現を避けるために回転行列から変換する方法としては，次の３つの方法がよく使われているみたいです．
- Quaternion を使ったパラメータ化
- Angle-Axis Representation を使ったパラメータ化
- 微小回転を用いたパラメータ化
Ceres-Solver ではデフォルトで Angle-Axis Representation が使われていたこともあり，今回は Angle-Axis Representation でやってみました．微小回転を用いたパラメータ化の説明については，金谷先生の下記の本がとても分かりやすかったです．
- 作者:健一, 金谷
- 発売日: 2019/07/27
- メディア: 単行本
Angle-Axis Representation を用いた回転のパラメータ化
Angle-Axis Representation を考えるために，ロドリゲスの式を導出します．この導出では，任意の回転軸（k）周りの任意の回転角（θ）の回転移動を回転軸ベクトル k と 回転各 θ を用いて表現します．
ロドリゲスの公式で，回転前の点 r を回転後の点 r' に変換させることができました．一方で，この回転と等価の回転行列 R を使っても点は変換できる（r' = Rr） となるはずなので，ロドリゲスの公式から等価な回転行列を求めます．ベクトルの外積計算を表現するために，外積計算用の行列を導入しています．
ということで，回転行列を回転軸と回転角を使って表現できるようになりました．が，回転軸と回転角で変数が計４つあります．もう一つ減らしたい．．．ということで，減らします．ここまでは回転軸ベクトルは単位ベクトルでしたが，回転軸ベクトルの大きさを回転角とすることによって変数を３つにします．
ふ～．できました．が，このままだと回転角が小さい，もしくは０の時に式が不定になってしまいます．つまり，回転角が０の時がこの表現方法の特異点ということになりますが，このままではまずいので，次にこれを除去します．
目次のページ
バンドル調整はシリーズ物として書いてまして，目次は下記のページになります．
daily-tech.hatenablog.com
１．バンドル調整 ～ モデル化，及び問題設定
２年前に「最適化計算５ バンドル調整 理論編１」としてエントリを書いていたのですが，今回はこの記事をリライトしています．
バンドル調整とは
三次元シーンを複数のカメラ・視点で撮影した時，全体的に「一番つじつまが合っている．」構成を求めるための手法です．ここで，「つじつまが合う」というのが何なのかを定義してやる必要があります．三次元復元の場合，「再投影誤差を小さくする．」ということがそれに該当します．（うーん．二年前に書いた表現ですが，なんだかうまく書き直せないのでそのままにします．）
バンドル調整のイメージ
３次元点と当該点が各カメラのスクリーンに映った様子を図示します．
それぞれのカメラに関して，３次元座標とスクリーン投影座標には下記の透視投影の関係が成立します．簡単のために，レンズの歪は考えていません．
ただ，ここで成立している関係はそれぞれのカメラ座標系に関してのものです．実際にバンドル調整をするときには基準座標を決めてあげないといけません．今回は簡単のためにカメラ１を基準座標として設定します．基準座標を合わせるために，それぞれの座標系であらわされている点 a の三次元座標を基準座標系（＝カメラ１）で表します．それぞれのカメラの位置がわかっていれば，カメラ間の相対位置関係から次のように変換できます．ここでは，カメラ間の相対位置関係が次のようにわかっているとします．
次に，カメラ間の相対位置関係を用いて点 a の座標変換をします．この変換で，「カメラ k から見た点 a の座標」を「基準座標での点 a の座標」を用いて表せるようになります．
各カメラで成立する透視投影の関係に，上スライドの点 a の座標変換式を代入すると，結果的に下記のようにまとまります．
上スライドの最後の式を用いれば，「カメラの３次元位置」，「カメラの内部パラメータ」，「被写体（点 a）の３次元位置」のすべてがわかっていれば，「被写体が写真のどこに写るか」がわかることになります．この式をもう少し書き出すと，，，
これで，スクリーン投影点の "モデル” ができたことになります．一方で，被写体が画像のどこに写っているかは実測できるので，ここまでの導出で被写体の画像座標に関して「実測値」と「予測値（モデル値）」がわかることになります．ここで，モデルが正確だと仮定すると，点 a の位置，各カメラの内部／外部パラメータが完全にあっていれば実測値と予測値は一致します．逆にずれが大きいと，どこかに誤差があることになります．パラメータの誤差は間接的（実測値と予測値の乖離が大きいか否か）にしかわかりませんが，次に，この「誤差の程度」を定義するために評価関数を定義します．
最小化したい評価関数・誤差関数
ここで「誤差の程度」を定義するために，下記の評価関数を使います．式の定義を見て頂ければわかるように，「実測値」と「予測値（モデル値）」が完全に一致すれば評価関数の値は０になります．つまり，評価関数の値が小さくなるほど，モデルに使用されている値が正確であるということになります．
ここまでの式導出の流れだと，
１．パラメータ（「カメラの３次元位置」，「カメラの内部パラメータ」，「被写体（点 a）の３次元位置」）がわかる．
２．モデルに値を代入して，予測値を計算する．
３．予測値と実測値を評価関数に代入して，どの程度の誤差になるか求める．
４．誤差が大きいので，手修正で（笑）ちょっとパラメータをいじってみる．そして２にもどる（笑）
だと思うのですが，バンドル調整では誤差関数の最適化をすることによって「手修正によらず（笑）」最適パラメータを求めます．うーん．いつものことながら，うまいことできているなあと感心します．
今回の問題設定のイメージ
今回の問題設定のイメージは，下記になります．
３次元空間では下記の様な設定になってまして，それぞれのカメラで撮影した円環の画像も載せています．
問題の前提
問題があまり複雑になるといけない一方で，実際に使用する仮定と大きくずれると良くないので，下記の前提でバンドル調整を実施しました．
下記の３点を既知とする．
１．画像に写っている点の画像座標．
２．３台のカメラの位置・角度．（バンドル調整を実施する前に，この値に誤差を載せます．）
３．円弧状の点の３次元位置．（バンドル調整を実施する前に，この値に誤差を載せます．）
カメラの内部パラメータは２種類あり，カメラ１とカメラ２が同じものを共有．カメラ３のみ異なる内部パラメータを保持．
ということで次のエントリに続きます．．．
目次のページ
バンドル調整はシリーズ物として書いてまして，目次は下記のページになります．
daily-tech.hatenablog.com