カメラ位置・姿勢推定0 PNP問題 外部パラメータ推定実験
PNP問題の総まとめとして,そろそろちょっと手を動かしてみようと思い,実験室(=リビング)で実験をすることにしました.
実験室の設定
まずは実験室の設定です.なんだか怪しい占いをしている部屋みたいな感じになってしまいましたが,一応キャリブレーションルームのつもりです.床面にグリーンの養生テープが貼られていますが,これは一マス50cmの間隔で貼っています.で,これだけだと一つの平面を構成する点群だけになってしまうので,高さをのある点をつくるために「南アルプスの天然水」を導入しました(笑).

南アルプスの天然水は,高さ31cmです.

カメラの搭載場所
カメラの搭載場所ですが,設定を簡単にするために世界座標の原点に設置しました.ただし,高さ(51cm)と俯角(12度)がつけられています.

キャリブルーム(実験室)の校正用写真
この画像を撮影したカメラの世界座標系での位置((0, 0.51, 0),俯角12度)が不明であるとして,計算から求めるのが最終目的です.

キャリブルーム写真 校正後写真
PNP問題のエントリでも書いたように,「内部パラメータは既知である」必要があるので,OpenCVのキャリブレーションツールを使って事前にキャリブレーションを完了させます.OpenCVでキャリブレーションした結果,カメラ行列は下記のようになりました.
カメラ行列
A = [[602.214, 0, 685.149], [0, 602.214, 527.226], [0, 0, 1]]
歪み係数
dist = [-0.2563, 0.0694, -0.00007838, -0.0005486, -0.008451]
上記の歪み係数を使って歪み補正した結果が下記の写真です.写真の端の歪みが取れていると思います.

キャリブルームの碁盤の目と該当箇所の画像座標
キャリブルーム各点の世界座標と歪み補正後の画像座標の関係を下記出してみました.青で書かれている座標が世界座標系からみた各点の座標,赤で書かれている点が画像座標系で見た各点の座標です.

上記の図より,19個の点の対応関係が求まります.
計算に使用する点
で,上記の図からわかった対応点を列挙すると,下記のようになります.ここで,正規化画像座標系でも座標を求めていますが,画像座標と正規化画像座標系でv軸とy軸の向きが逆であることには要注意です.

PNP問題を解く!
DLT法で解く方程式
以前の下記エントリでDLT法で解く方程式を導出しましたが,復習です.
daily-tech.hatenablog.com
Pythonスクリプト
import numpy as np
world = np.array(\
[\
[-0.50, 0.00, 0.50], \
[ 0.00, 0.00, 0.50], \
[ 0.50, 0.00, 0.50], \
[-0.50, 0.00, 1.00], \
[ 0.00, 0.00, 1.00], \
[ 0.50, 0.00, 1.00], \
[-1.00, 0.00, 1.50], \
[-1.00, 0.31, 1.50], \
[-0.50, 0.00, 1.50], \
[ 0.00, 0.00, 1.50], \
[ 0.50, 0.00, 1.50], \
[ 1.00, 0.00, 1.50], \
[ 1.00, 0.31, 1.50], \
[-0.50, 0.00, 2.00], \
[-0.50, 0.31, 2.00], \
[ 0.00, 0.00, 2.00], \
[ 0.00, 0.31, 2.00], \
[ 0.50, 0.00, 2.00], \
[ 0.50, 0.31, 2.00], \
])
img = np.array(\
[\
[ 175, 946], \
[ 715, 940], \
[ 1279, 939], \
[ 417, 686], \
[ 705, 683], \
[ 999, 676], \
[ 311, 594], \
[ 288, 478], \
[ 504, 591], \
[ 703, 591], \
[ 903, 585], \
[ 1104, 581], \
[ 1115, 460], \
[ 549, 541], \
[ 540, 451], \
[ 702, 539], \
[ 698, 447], \
[ 852, 535], \
[ 854, 443], \
])
normalized_img = np.array(\
[\
[-0.85, -0.85], \
[ 0.05, -0.84], \
[ 0.99, -0.84], \
[-0.45, -0.42], \
[ 0.03, -0.42], \
[ 0.52, -0.40], \
[-0.62, -0.27], \
[-0.66, -0.08], \
[-0.30, -0.26], \
[ 0.03, -0.26], \
[ 0.36, -0.25], \
[ 0.70, -0.25], \
[ 0.71, -0.05], \
[-0.23, -0.18], \
[-0.24, -0.03], \
[ 0.03, -0.18], \
[ 0.02, -0.02], \
[ 0.28, -0.17], \
[ 0.28, -0.02], \
])
## Create M Matrix that will be solved by SVD.
def createMMatrix(imgPnt, worldPnt):
pntNum = imgPnt.shape[0]
M = np.empty((0, 12 + pntNum))
for i in range(imgPnt.shape[0]):
Xw = worldPnt[i][0]
Yw = worldPnt[i][1]
Zw = worldPnt[i][2]
x = imgPnt[i][0]
y = imgPnt[i][1]
vec = np.zeros((3, 12 + pntNum))
# For X
vec[0, 0] = Xw
vec[0, 1] = Yw
vec[0, 2] = Zw
vec[0, 3] = 1.0
vec[0, 12 + i] = -x
# For Y
vec[1, 4] = Xw
vec[1, 5] = Yw
vec[1, 6] = Zw
vec[1, 7] = 1.0
vec[1, 12 + i] = -y
# For Z
vec[2, 8] = Xw
vec[2, 9] = Yw
vec[2, 10] = Zw
vec[2, 11] = 1.0
vec[2, 12 + i] = -1
M = np.append(M, vec, axis=0)
return M
def calculateProjectionMatrix(M):
U, S, V = np.linalg.svd(M, full_matrices=True)
num = 1
v = V[V.shape[0] - num]
lamda = v[V.shape[0] - num]
sign = 1
if (lamda < 0):
sign = -1
P = sign * np.array([[v[0], v[1], v[2], v[3]], [v[4], v[5], v[6], v[7]], [v[8], v[9], v[10], v[11]]])
return P
def calculateRotationMatrixViaQRFactorization(P):
A1 = np.matrix(P[0, 0:3])
A2 = np.matrix(P[1, 0:3])
A3 = np.matrix(P[2, 0:3])
f = np.linalg.norm(A3)
R3 = A3 / f
e = A2 * R3.T
d = np.linalg.norm(A2 - e * R3)
R2 = (A2 - e * R3) / d
c = A1 * R3.T
b = A1 * R2.T
a = np.linalg.norm(A1 - b * R2 - c * R3)
R1 = (A1 - b * R2 - c * R3) / a
#print()
#print("Rotation Matrix R : ")
R = np.zeros((0, 3))
R = np.append(R, R1, axis=0)
R = np.append(R, R2, axis=0)
R = np.append(R, R3, axis=0)
#print(R)
K = np.matrix([[a, b, c], [0, d, e], [0, 0, f]])
return R, K
if __name__ == "__main__":
print("Solve PNP Problem!")
# 1. Create M Matrix.
M = createMMatrix(normalized_img, world)
# 2. Calculate Projection Matrix
P = calculateProjectionMatrix(M)
# 3. Calculate R and K matrix via QR factorization.
R, K = calculateRotationMatrixViaQRFactorization(P)
print("Camera Intrisic Matrix")
print(K / K[2, 2])
print()
# 5. Translation found by P = [KR KT] -> T = inv(K) * P[:, 3]
print("Camera Translation : ")
print(np.linalg.inv(K) * np.matrix(P[:, 3]).T)
print()
print("Camera Rotation : ")
print(R)
上記スクリプトはPNP問題実験編2で用いたものと同じですが,実行すると下記の結果が出てきます.
Translation に関しても,Rotation に関しても,問題設定のもの(高さ 51 cm, 俯角 12deg (cos(12deg) = 0.978) )と同じ結果が出ています.
また,正規化画像座標を用いたので,カメラの内部パラメータ行列はほぼ単位行列になっていることがわかります.
Camera Intrisic Matrix [[ 1.02943989 -0.02945167 0.00755392] [ 0. 0.99584322 -0.09206592] [ 0. 0. 1. ]] Camera Translation : [[ 0.00254687] [-0.51267888] [ 0.07332725]] Camera Rotation : [[ 0.99960549 -0.02382944 0.01486711] [ 0.02095918 0.98523074 0.16994441] [-0.01869722 -0.16956576 0.9853415 ]]
カメラの位置・姿勢推定2 PNP問題 実験編2
前回の下記エントリ,
daily-tech.hatenablog.com
では,OpenCVのSolvePNP関数を用いて世界座標が既知の7点,およびその投影点を用いてカメラ位置を計算しました.
今回のエントリでは,下記のブログでまとめたPNP問題の理論式をPythonで実装して同じことをやりたいと思います.
daily-tech.hatenablog.com
問題設定は実験編1と同じで下記のとおりです.
0.問題のイメージ図
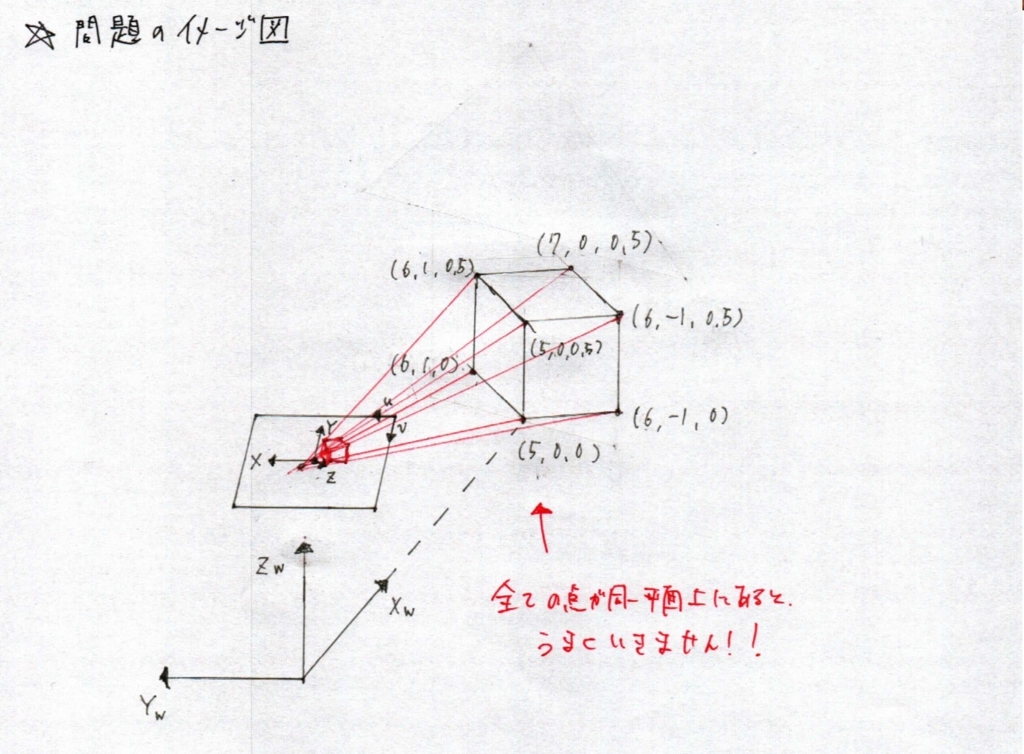
※すべての点が同一平面上にあると,下記のサンプルコードではうまくいきません!これではまって数週間....
1.世界座標が既知の7点を,位置が既知のカメラに投影した時の画像座標を求める.
ここでは,投影画像座標を求めます.問題を簡単にするために,画像にレンズひずみはないものとし,内部パラメータは下記のように定義します.
画像幅 :640pix
画像高さ:480pix
主点x :320
主点y :240
焦点距離:160pix
カメラ高さ:1m
カメラ角度:俯角30度
投影点は OpenCVの projectPoints 関数を使ってやれば簡単にできます.コードは実験編1を参照ください.
2.世界座標,画像座標が既知の点7点をつかってカメラの位置を求める
今度は上記の結果を使ってカメラ位置を求めます.下記は理論編で導いた数式を Python でコーディングしたものです.
import numpy as np
world = np.array(\
[\
( 5.00, 0.00, 0.00), \
( 5.00, 0.00, 0.50), \
( 6.00, -1.00, 0.00), \
( 6.00, -1.00, 0.50), \
( 6.00, 1.00, 0.00), \
( 6.00, 1.00, 0.50), \
( 7.00, 0.00, 0.50), \
])
img_pnt = np.array(\
[\
(320. , 294.12609945), \
(320. , 312.2071607), \
(291.91086401, 299.94150262), \
(290.62146125, 315.41433581), \
(348.08913599, 299.94150262), \
(349.37853875, 315.41433581), \
(320. , 317.74146755), \
])
f = 160
Cu = 320
Cv = 240
## Calculate Normalize Point
def calculateNormailzePnt(img_pnt):
normalized_img = np.zeros((0, 2))
for i in range(img_pnt.shape[0]):
vec = np.zeros((1, 2))
vec[0][0] = (img_pnt[i][0] - Cu) / f
vec[0][1] = (img_pnt[i][1] - Cv) / f
normalized_img = np.append(normalized_img, vec, axis = 0)
return normalized_img
## Create M Matrix that will be solved by SVD.
def createMMatrix(imgPnt, worldPnt):
pntNum = imgPnt.shape[0]
M = np.empty((0, 12 + pntNum))
for i in range(imgPnt.shape[0]):
Xw = worldPnt[i][0]
Yw = worldPnt[i][1]
Zw = worldPnt[i][2]
x = imgPnt[i][0]
y = imgPnt[i][1]
vec = np.zeros((3, 12 + pntNum))
# For X
vec[0, 0] = Xw
vec[0, 1] = Yw
vec[0, 2] = Zw
vec[0, 3] = 1.0
vec[0, 12 + i] = -x
# For Y
vec[1, 4] = Xw
vec[1, 5] = Yw
vec[1, 6] = Zw
vec[1, 7] = 1.0
vec[1, 12 + i] = -y
# For Z
vec[2, 8] = Xw
vec[2, 9] = Yw
vec[2, 10] = Zw
vec[2, 11] = 1.0
vec[2, 12 + i] = -1
M = np.append(M, vec, axis=0)
return M
def calculateProjectionMatrix(M):
U, S, V = np.linalg.svd(M, full_matrices=True)
num = 1
v = V[V.shape[0] - num]
#print()
#print("Eigen Value Matrix S : ")
#print(S)
#print()
#print("Eigen Vector Matrix V : ")
#print(V)
#print()
#print("Eigen Vector with Minimum Eigen Value : ")
#print(v)
lamda = v[V.shape[0] - num]
#print()
#print("Lamda with minimum Eigen Value : ")
#print(lamda)
# lamda has to be positive!
if (lamda < 0):
sign = -1
#print()
#print("Projection Matrix P : ")
P = sign * np.array([[v[0], v[1], v[2], v[3]], [v[4], v[5], v[6], v[7]], [v[8], v[9], v[10], v[11]]])
#print(P)
return P
def calculateRotationMatrixViaQRFactorization(P):
A1 = np.matrix(P[0, 0:3])
A2 = np.matrix(P[1, 0:3])
A3 = np.matrix(P[2, 0:3])
f = np.linalg.norm(A3)
R3 = A3 / f
e = A2 * R3.T
d = np.linalg.norm(A2 - e * R3)
R2 = (A2 - e * R3) / d
c = A1 * R3.T
b = A1 * R2.T
a = np.linalg.norm(A1 - b * R2 - c * R3)
R1 = (A1 - b * R2 - c * R3) / a
#print()
#print("Rotation Matrix R : ")
R = np.zeros((0, 3))
R = np.append(R, R1, axis=0)
R = np.append(R, R2, axis=0)
R = np.append(R, R3, axis=0)
#print(R)
K = np.matrix([[a, b, c], [0, d, e], [0, 0, f]])
return R, K
if __name__ == "__main__":
print("Solve PNP Problem!")
# 1. Calculate Normalize Coordinate.
normalized_img = calculateNormailzePnt(img_pnt)
#M = createMMatrix(normalized_img, world)
# 2. Create M Matrix that will be solved by SVD.
M = createMMatrix(img_pnt, world)
# 3. Calculate Projection Matrix
P = calculateProjectionMatrix(M)
# 4. Calculate R and K matrix via QR factorization.
R, K = calculateRotationMatrixViaQRFactorization(P)
print("Camera Intrisic Matrix")
print(K / K[2, 2])
print()
# 5. Translation found by P = [KR KT] -> T = inv(K) * P[:, 3]
print("Camera Translation : ")
print(np.linalg.inv(K) * np.matrix(P[:, 3]).T)
print()
print("Camera Rotation : ")
print(R)
最終的には,カメラの内部パラメータ行列 K と並進ベクトル T が下記のように求まります.
仮想的に設定した, f = 160, Cu = 320, Cv = 240 が求まっていることがわかります.また,位置と回転に関しても「カメラ座標系からみた世界座標」が正しく求まっています.
Camera Intrisic Matrix [[ 1.60000000e+02 1.21914379e-08 3.20000000e+02] [ 0.00000000e+00 1.60000000e+02 2.40000000e+02] [ 0.00000000e+00 0.00000000e+00 1.00000000e+00]] Camera Translation : [[ -3.13782333e-11] [ -8.66025401e-01] [ 5.00000005e-01]] Camera Rotation : [[ -2.33381743e-10 1.00000000e+00 2.54500444e-11] [ 4.99999998e-01 9.46498690e-11 8.66025405e-01] [ 8.66025405e-01 2.14840023e-10 -4.99999998e-01]]
同次式の最小二乗問題
同次式(Homogeneous Equations)とは
同次式とは,すべての項の次数が等しい多項式を言います.下記に一例を示します.

逆に,下記のような例は項の次数が異なっているため,非同次式(Non Homogeneous Equations)といいます.

同次式の最小二乗問題
非同次式の最小二乗法問題は, Ax =b を満たすベクトル x を求めるという問題で,実用上多く見かけます.通常コンピュータビジョンでこの問題を解くときは,方程式の未知数よりも多いデータが与えられるけどもそれぞれのデータが少しずつノイズを含んでいるために最小二乗法を用いて誤差が一番少ないベクトル x を求めます.今回の同次式の最小二乗法問題では, Ax = 0 となるベクトル x を求めます.x = 0 は当たり前に成り立つので,求めたい解は x = 0 以外のものになります.例としては,複数の二次元点が与えられたときに,近似直線を求める問題です.

また,コンピュータビジョンでは楕円当てはめをすることがありますが,これも同次式の最小二乗問題として考えることができます.

同次式の最小二乗問題の特徴
当時式の最小二乗解には次の二つの特徴があります.
1.x = 0 は常に解になる.が,これは当たり前.
2.x ≠ 0 が解になったばあい,このスカラー倍 kx も同様に解になる.
上記の2番の特徴から,ベクトル x は大きさが不定になることがわかります.つまり,もう一つ条件を付けてあげる必要があります.追加の条件としては,下記の条件がよくつかわれます.

同次式の最小二乗問題の定義
下記,同次式の最小二乗問題の定義です.

同次式の最小二乗問題の解
ここでようやく特異値分解を使って解を求めます.簡単のために,上記ノートの B を I とします.この簡単化によって,解の不定性を取り除くための条件は「解ベクトルのノルムが1となるもの」となります.
行列 A が下記のように特異値分解できたとすると,,,,

このAの特異値分解を用いて,最小化すべき式 ||Ax|| = 0 を書き直すと下記のようになります.

最終的に y を求める問題になりましたが,行列 S は 行列 A の特異値を対角成分に持つ行列で,かつ || y || = 1 より y は単位ベクトルとなるので,y は A の最小特異値に対応するベクトルとなり,肝心の x は下記のようになります.

線形代数 もろもろ雑多なメモ
線形代数の勉強中....メモ.
固有値とランクの関係
固有値
行列Aに対して,

となる定数 λ とベクトル x が存在するとき,定数 λ をAの固有値, x を固有ベクトルという.
これをもう少し変形していくと...

つまり,
1.固有ベクトル x は行列 A - λI の零空間に存在している.
2.λ は A - λI が零空間を持つように決められる.
といえる.
直行行列 (Orthogonal Matrix)
n 次元単位直交列ベクトル u1, u2, .... un を列とする下記の n x n 行列を直交行列と呼ぶ.

直交行列は単位直交列ベクトルから構成されており,転置行列が逆行列となる.

ベクトルに対して直交行列をかけても,ベクトルの長さ,角度,内積は保存される.

対称行列 (Symmetric Matrix)
Aという n x n 行列を考えるたときに,自身の転置行列 ATと等しいような行列を対称行列という.具体的には...

特記事項
1.対称行列の固有値はすべて実数であり,対応する固有ベクトルも実数ベクトルである.
2.対称行列の異なる固有値に対応する固有ベクトルは互いに直交する.
3.対称行列の0でない固有値の個数は,その行列のランクに等しい.つまり, n x n 対称行列が正則行列である必要十分条件は,すべての固有値が 0 でないことである.
対角化(Diagonalization)
n x n 行列Aが n 本の線形独立な固有ベクトルを持っているとすると,行列Aは下記のように対角化できる.この時対角化に用いる行列SはAの固有ベクトルを列ベクトルにもつ.

特記事項
1.n x n 行列Aの固有値 λ1, λ2, ... λn がすべて異なる場合,n 個の固有ベクトルはすべて線形独立であり,この行列Aは対角化可能である.
2.n x n 行列Aの固有値 λ1, λ2, ... λn の中で同じものがあったとしても,この行列Aが対角化可能な場合もある.
3.n x n 行列の中で,n 個の線形独立な固有ベクトルを持たないものもある.つまり,対角化できない行列も存在する
欧州出張2・3・4日目 ドイツ編
ということで,表題のとおり欧州出張後半はドイツに行ってきました.場所としては,2・3日目にはベルリンに,4日目にはフランクフルト滞在でした.フランクフルトはオフィスと空港の往復だけだったのですが,ベルリンでは少しだけ時間があったので観光しました.
ブランデンブルク門
うーん.撮影ミスですね.暗くなってしまいました.Wikipedia先生によると,もともと平和の象徴として作成された門だったけど,ベルリンがナポレオンに征服されたときに門の上のヴィクトリア像がフランスへ戦利品として持ち帰られたそう.そのあと,ナポレオン戦争でナポレオンが敗北した後に戻されたそうです.

ベルリン大聖堂
世界遺産だそうです.中に入るべきだったかなー.7ユーロ位したことと,一緒に行ったメンバーが乗り気じゃなかったのであきらめました.

ベルリン国会議事堂

ベルリンの壁
ベルリンの壁を見に行ったときにベルリンの壁記念館というとこにも行ったんですが,歴史に翻弄された当時の人々のことを考えると思わず泣きそうになってしまいました.沖縄一人旅で行ったひめゆりの塔でもそうですが,最近よく泣いてしまいます...おそらくおっさん化が始まっているのかと.
実はベルリンの壁のことをちゃんと理解してませんでした.ベルリンは地理的には東ドイツにあるのですが,ドイツの首都であったために重要性が高く西側諸国と東側諸国とでベルリンを分割しました.なので,地理的には東ドイツにあるけれども,ベルリンの半分(西ベルリン)は西側諸国に統治されていました.西ベルリンは当然ながら地理的には東ドイツにあるのでソ連をはじめとする東側諸国と国境を接しており,この国境に作られた壁のことを「ベルリンの壁」というようです.

欧州出張1日目 スイス編
不覚にも2月になって仕事がバタバタし始めてしまい...ブログの更新が滞ってしまいました.
個人的には仕事なんかよりロボットのほうがいろんな意味で数倍大切なんですが(笑),やっぱり仕事が詰まってくると仕事してしまいますね....サラリーマンの悲しき性なんだと思います...
で,表題のとおりヨーロッパに弾丸出張に行ってきました!以前,今の会社に入る前にドイツに半年ぐらい出向していて,「もうヨーロッパはおなか一杯...」だったのですが,たまに行くのはそれはそれで悪くないですね.
久々の成田です!乗った飛行機は,最安のスイス航空ですが..

成田からのチューリッヒです.英語発音すると「チューリッヒ」じゃなくて「ズーリック」ですが,外国人と話しているときに「ズーリック」って発音している自分に毎回酔っているのは,ここだけの話です(笑)

以前にも,ズーリック(笑)で飛行機を乗り換えたことはあったんですが,今回は宿泊しました.ついでに街を散策しましたが,地震がないせいか建物が古い&美しいですね.

チューリッヒ中央駅です.

宿泊したチューリッヒのホテルです.

チューリッヒの街並み@ナイトです.

夕食にはチーズフォンデュを食べました.チーズはとてもおいしかったんですが,ディップするものが「パン」「ポテト」だけなんですよね...もうちょっといろいろあればもっと楽しめると思うんですけどね.

仕事(観光?)を終えて,チューリヒからベルリンへ移動です.

というこで,次はベルリン編です!
カメラの位置・姿勢推定2 PNP問題 実験編1
下記のエントリで透視投影モデル,およびその計算式を導入し,
daily-tech.hatenablog.com
下記のエントリでPNP問題とその解法を導入しました.
daily-tech.hatenablog.com
今回のエントリとその次のエントリで実際に PNP 問題を解いてみたいと思います.両方のエントリで同じ問題「1.世界座標が既知の7点を,位置が既知のカメラに投影した時の画像座標を求める.」と「2.世界座標,画像座標が既知の点7点をつかってカメラの位置を求める」を扱いますが,今回のエントリでは OpenCV の関数を用いて,次回のエントリでは自作のプログラムで問題を解きます.
0.問題のイメージ図

※以前アップしていた絵だとすべての点が同一平面上にあるので,自作のPNP関数ではうまくいきませんでした.OpenCVのsolvePNPでは,同一平面上にあっても解は求まりましたが.
1.世界座標が既知の7点を,位置が既知のカメラに投影した時の画像座標を求める.
ここでは,投影画像座標を求めます.問題を簡単にするために,画像にレンズひずみはないものとし,内部パラメータは下記のように定義します.
画像幅 :640pix
画像高さ:480pix
主点x :320
主点y :240
焦点距離:160pix
カメラ高さ:1m
カメラ角度:俯角30度
ここでは,投影点を求めるために,OpenCV の projectPoint 関数を使います.下記, Python のスクリプトです.
ここで注意が必要なのは,R, t は「カメラ座標から見たワールド座標の位置」でなければいけないことと,オイラー角表現を用いているので回転行列の掛け算が Rx * Ry * Rz になってます.
import numpy as np
import cv2
import math
world = np.array(\
[\
( 5.00, 0.00, 0.00), \
( 5.00, 0.00, 0.50), \
( 6.00, -1.00, 0.00), \
( 6.00, -1.00, 0.50), \
( 6.00, 1.00, 0.00), \
( 6.00, 1.00, 0.50), \
( 7.00, 0.00, 0.50), \
])
# Camera Extrinsic Parameter
xRadEuler_C2W = -120 / 180 * math.pi
yRadEuler_C2W = 0 / 180 * math.pi
zRadEuler_C2W = -90 / 180 * math.pi
Rx = np.matrix([[1, 0, 0], [0, math.cos(xRadEuler_C2W), -math.sin(xRadEuler_C2W)], [0, math.sin(xRadEuler_C2W), math.cos(xRadEuler_C2W)]])
Ry = np.matrix([[ math.cos(yRadEuler_C2W), 0, math.sin(yRadEuler_C2W)], [0, 1, 0], [-math.sin(yRadEuler_C2W), 0, math.cos(yRadEuler_C2W)]])
Rz = np.matrix([[ math.cos(zRadEuler_C2W), -math.sin(zRadEuler_C2W), 0], [ math.sin(zRadEuler_C2W), math.cos(zRadEuler_C2W), 0], [0, 0, 1]])
# Notice : Rotation Matrix from Euler Angle.
R = Rx * Ry * Rz
# tvec is expressed wrt camra coord.
tvec = R * np.matrix((0, 0, -1)).T
# Camera Intrinsic Paramter
dist_coeffs = np.zeros((5, 1))
width = 640
height = 480
focal_length = 160
center = (width / 2, height / 2)
camera_matrix = np.array([[focal_length, 0, center[0]],
[0, focal_length, center[1]],
[0, 0, 1]], dtype = "double")
if __name__ == "__main__":
print("Calculate Projected Point")
print("\nExtrinsic Paramter")
print("Translation")
print(tvec)
print("Rotation")
print(R)
print("\nCamera Matrix : ")
print(camera_matrix)
print("\nDistortion Coefficient")
print(dist_coeffs)
print("\nGenerate Rotation Vector from Rotation Matrix")
rvec, jacob = cv2.Rodrigues(R)
print(rvec)
print("\nProject Point on Screen")
result = cv2.projectPoints(world, rvec, tvec, camera_matrix, None)
for n in range(len(world)):
print(world[n], '==>', result[0][n])
上記スクリプトを実行すると,下記の結果(画像座標での7点の投影位置)が得られます.
Project Point on Screen [ 5. 0. 0. ] ==> [[ 320. 294.12609945]] [ 5. 0. 0.5 ] ==> [[ 320. 312.2071607]] [ 6. -1. 0. ] ==> [[ 291.91086401 299.94150262]] [ 6. -1. 0.5 ] ==> [[ 290.62146125 315.41433581]] [ 6. 1. 0. ] ==> [[ 348.08913599 299.94150262]] [ 6. 1. 0.5 ] ==> [[ 349.37853875 315.41433581]] [ 7. 0. 0.5 ] ==> [[ 320. 317.74146755]]
2.世界座標,画像座標が既知の点7点をつかってカメラの位置を求める
今度は逆に,上記の結果を使ってカメラ位置を求めます.
import numpy as np
import cv2
import math
world = np.array(\
[\
( 5.00, 0.00, 0.00), \
( 5.00, 0.00, 0.50), \
( 6.00, -1.00, 0.00), \
( 6.00, -1.00, 0.50), \
( 6.00, 1.00, 0.00), \
( 6.00, 1.00, 0.50), \
( 7.00, 0.00, 0.50), \
])
img_pnts = np.array(\
[\
(320. , 294.12609945), \
(320. , 312.2071607), \
(291.91086401, 299.94150262), \
(290.62146125, 315.41433581), \
(348.08913599, 299.94150262), \
(349.37853875, 315.41433581), \
(320. , 317.74146755), \
])
# Camera Intrinsic Paramter
dist_coeffs = np.zeros((5, 1))
width = 640
height = 480
focal_length = 160
center = (width / 2, height / 2)
camera_matrix = np.array(
[[focal_length, 0, center[0]],
[0, focal_length, center[1]],
[0, 0, 1]], dtype = "double"
)
if __name__ == "__main__":
print("Solve Perspective N Point Problem")
print("\nCamera Matrix : ")
print(camera_matrix)
print("\nDistortion Coefficient")
print(dist_coeffs)
(success, rot_vec, trans_vec) = cv2.solvePnP(world, img_pnts, camera_matrix, dist_coeffs, flags=cv2.SOLVEPNP_ITERATIVE)
print("\nTranslation Vector")
print(trans_vec)
print("\nRotation Vector")
print(rot_vec)
print("\nRotation Matrix")
R, jacob = cv2.Rodrigues(rot_vec)
print(R)
上記スクリプトを実行すると,下記の結果(画像座標での7点の投影位置)が得られます.もともとのカメラ位置が求まりました.
Translation Vector [[ -8.87481507e-11] [ -8.66025403e-01] [ 4.99999999e-01]] Rotation Vector [[-1.58351453] [-1.58351453] [-0.91424254]] Rotation Matrix [[ 1.53020929e-11 1.00000000e+00 -5.93469718e-13] [ 5.00000000e-01 -7.13717974e-12 8.66025404e-01] [ 8.66025404e-01 -1.35487732e-11 -5.00000000e-01]]
次のエントリでは,自作のアルゴリズムでPNP問題を解いてみます.それではまた!







