ハフ変換
さあ,,,つくばチャレンジ本番までついに2週間です...つくばチャレンジ本番2週間前にこんな基礎的なことやってていいのかなあ...と思いつつ,どうしてもハフ変換が必要になったので,思い切って実装しました.OpenCVとかにも実装があるのですが,どうしても処理途中の中間データが必要だったので,思い切って作ってしまいました.ただ,計算速度が遅いので必要に応じて改善が必要です.実際のコードは下記のリポジトリに置いてあります.
0.ハフ変換とは
画像認識って,文字通り画像の中に写っているものを”認識”することだと思います.自動運転の車だったら道路を走っている人やほかの車を"認識"しなければいけません.これと同様に(だいぶ簡単ですが,,,,),今回のコードでは,画像の中にある"直線"を認識します.ハフ変換を使えば,円,楕円,直線などの特定の形状を認識することができます.
1.今回の画像
ペイントで書いた自分の絵ですが,今回は超シンプルに下記の絵の中に存在する黒い線をプログラムに認識させます.
2.考え方
2.1 直線の方程式
ハフ変換はいろんなサイトで説明されていると思うので,手短にちょっとだけ備忘のために書き残しておきます.一般に直線は下記の式で表現できます.
ax + by + c = 0
これは小学校で習う一次関数の式で,下記のイメージです.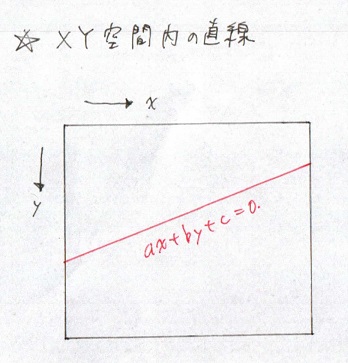
ただし,今回の目的は直線らしきものが含まれている画像を Input としてうけとった時に,その直線を認識することが目的です.そのため,当たり前ですが事前に直線の式はわかりません.もらった画像を調べて,そこに映っているかもしれない直線を探す必要があります.ここで,上の直線の式の見方を変えると....
(a/c) x + (b/c) y + 1 = 0
上式の二つの変数要素 (a/c,b/c) が決まれば,直線は一意に決まります.つまり,画像をスキャンしていって直線(=二つの変数要素 (a/c, b/c))に対して投票することができれば,画像に含まれている直線を認識することができそうです.
2.2 (ρ,θ) を使った直線の表現方法
で,二つの変数要素 (a/c,b/c) は実際のところどういう意味があるのか?ということを説明します.
直線の式の見方を少し変えて,ハフ変換中心を (0, 0) として,中心から直線までの距離を ρ ,x軸とのなす角を θ とすると,下記のように図示できます.
上図に赤で数式を書きましたが,このように表現すると結果的に数式が
(a/c) x + (b/c) y + 1 = 0
と同じ形になっていることがわかります.ということで,二つの変数要素 (a/c,b/c) は幾何学的には上記説明のような意味を持っており, (ρ,θ) が決まれば直線がただ一つ求まるということがわかります.
2.3 (ρ,θ) への投票
次に,どうやって (ρ,θ) 空間に投票するか?という問題ですが,ここは力ずくで投票します.下図で簡単に説明します.
1.画像の左上から右下まですべての画素を見る.
2.対象画素(下図の場合は4点)があった場合,下記の数式を用いて (ρ,θ) 空間に投票する.θは一解像度ずつ動かして,対象範囲(0 < θ < 180°)すべてをカバーする.
ρ = x * cosθ + y * sinθ
3.(ρ,θ)空間内で一番投票スコアが大きいものを最も有力な直線として採用する.

結局2のステップがキモになってます.対象画素で投票する場合,この画素を通るすべての角度の直線に投票します.対象画素が上図のようなパターンだった場合は,赤でかかれた線分が結局同じ直線(ρ,θ)になるので,ほかの候補直線よりも投票値がおおきくなって選択される.という流れです.
で,投票のための探索範囲ですが,対象画像中で取りうる ρ の最大値と直線の対称性を考えると,下記の図のようになります.

3.処理の流れ
で,肝心のコードの話です.
3.1 二値化画像の生成
必ずしも二値化画像にする必要はないかもしれないですが,簡単のために二値化しています.最終的にハフ変換される画像に関しては,0以外の値が対象画素としてみなされています.
cv::threshold(img, img, 50, 255, cv::THRESH_BINARY); cv::bitwise_not(img, img);

3.2 対象画素の投票
2.3で説明した(ρ,θ)空間への投票です.OpenCVだと,投票空間の結果が外部から取得できないので今回自作しました.
void HoughTrans::vote_rho_theta(cv::Mat &gray_img) {
// Initialize Buffer.
rho_theta = 0;
unsigned char * const img_pnt = gray_img.data;
int * const vote_st_pnt = reinterpret_cast<int *>(rho_theta.data);
// Outer loop for image
for (int v = 0; v < gray_img.rows; v++) {
for (int u = 0; u < gray_img.cols; u++) {
unsigned char val = *(img_pnt + v * gray_img.cols + u);
if (val >= vote_thresh) {
// Inner loop for voting
for (int theta_col = 0; theta_col < rho_theta.cols; theta_col++) {
// Rho-Theta Calculation
double theta = theta_res * theta_col * M_PI / 180.0;
double rho_abs = std::abs(u * cos(theta) + v * sin(theta));
if (rho_abs <= rho_max) {
// Hough Vote
int rho_row = std::abs(static_cast<int>(rho_abs / rho_res));
int *tgt_pnt = vote_st_pnt + rho_row * rho_theta.cols + theta_col;
*tgt_pnt = *tgt_pnt + 1;
}
}
}
}
}
}
3.3 上位直線の取得
(ρ,θ)空間の投票結果画像を用いて,投票結果が上位の直線を取得します.ちょっとここは書き方がいけてないかも.
void HoughTrans::get_top_ranked_lines(std::vector<LineElem> &lines) {
lines.clear();
int * const vote_st_pnt = reinterpret_cast<int *>(rho_theta.data);
for (int v = 0; v < rho_theta.rows; v++) {
for (int u = 0; u < rho_theta.cols; u++) {
double rho = v * rho_res;
double theta = u * theta_res;
int score = *(vote_st_pnt + v * rho_theta.cols + u);
if (score <= score_thresh) {
continue;
}
LineElem line2(rho, theta, score);
LineElem line = line2;
lines.push_back(line);
}
}
std::sort(lines.begin(), lines.end());
}
3.4 (ρ,θ)の値を用いて,結果を描画.
最終結果の描画です.
void calc_pnt_in_img(double rho, double theta, cv::Point2i &p1, cv::Point2i &p2) {
int x1, y1, x2, y2;
double theta_rad = theta * M_PI / 180.0;
if ((theta < 45.0) || (135.0 < theta)) {
y1 = -10000;
y2 = 10000;
x1 = -(sin(theta_rad)/cos(theta_rad)) * y1 + rho / cos(theta_rad);
x2 = -(sin(theta_rad)/cos(theta_rad)) * y2 + rho / cos(theta_rad);
} else {
x1 = -10000;
x2 = 10000;
y1 = -(cos(theta_rad)/sin(theta_rad)) * x1 + rho / sin(theta_rad);
y2 = -(cos(theta_rad)/sin(theta_rad)) * x2 + rho / sin(theta_rad);
}
p1.x = x1;
p1.y = y1;
p2.x = x2;
p2.y = y2;
}