2.バンドル調整 ~ 回転のパラメータ化
透視投影の式
前回エントリで扱ったモデル化で,カメラの透視投影の式を導出しました.下図のように基準座標となるカメラを決定すると,
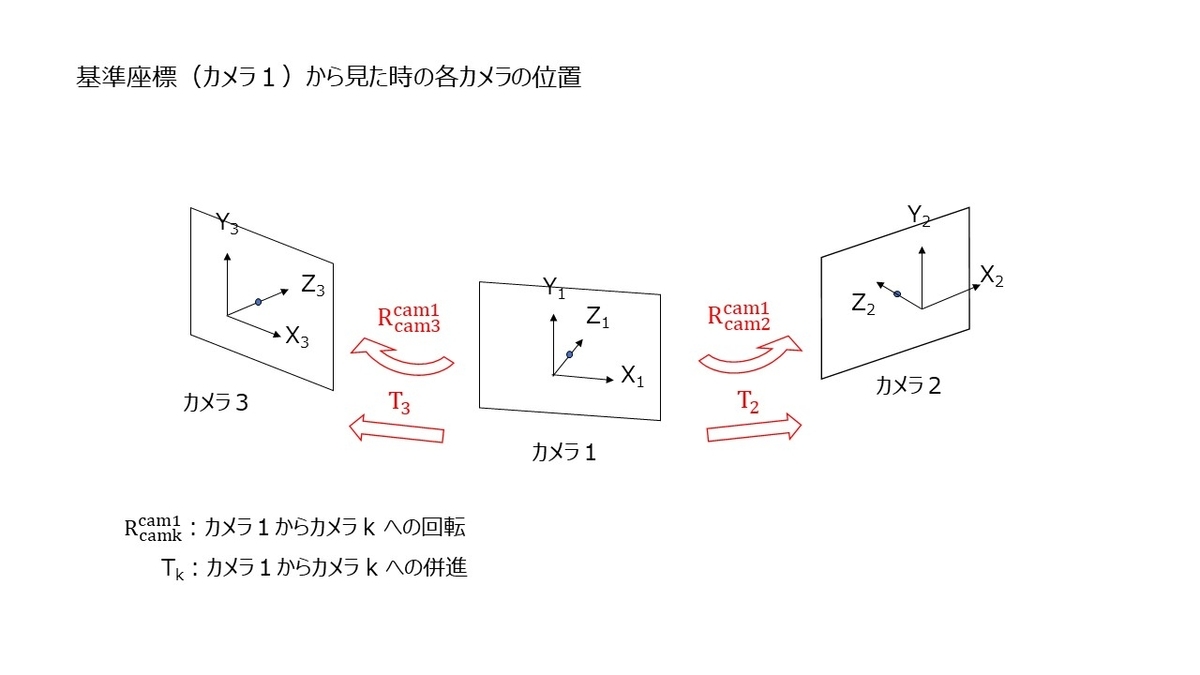
カメラの投影点を求めるためには下記の式を使う必要がありました.

ここで,各変数の自由度は次のようになります.
- 各カメラの併進ベクトル Tk : 自由度3
- 各カメラの内部パラメータ行列 Kk : 自由度5
- 各カメラの併進ベクトル Rk : 自由度3
併進ベクトル,内部パラメータ行列に関しては,設定した変数の数がそのまま自由度となっています.一方で,回転行列は 3x3 行列で表現しているので,一見すると変数は9個あるように見えますが,回転の自由度は3なので冗長な表現となっていることがわかります.
回転のパラメータ化の必要性
冗長な表現を避けるために回転行列から変換する方法としては,次の3つの方法がよく使われているみたいです.
- Quaternion を使ったパラメータ化
- Angle-Axis Representation を使ったパラメータ化
- 微小回転を用いたパラメータ化
Ceres-Solver ではデフォルトで Angle-Axis Representation が使われていたこともあり,今回は Angle-Axis Representation でやってみました.微小回転を用いたパラメータ化の説明については,金谷先生の下記の本がとても分かりやすかったです.

- 作者:健一, 金谷
- 発売日: 2019/07/27
- メディア: 単行本
Angle-Axis Representation を用いた回転のパラメータ化
Angle-Axis Representation を考えるために,ロドリゲスの式を導出します.この導出では,任意の回転軸(k)周りの任意の回転角(θ)の回転移動を回転軸ベクトル k と 回転各 θ を用いて表現します.
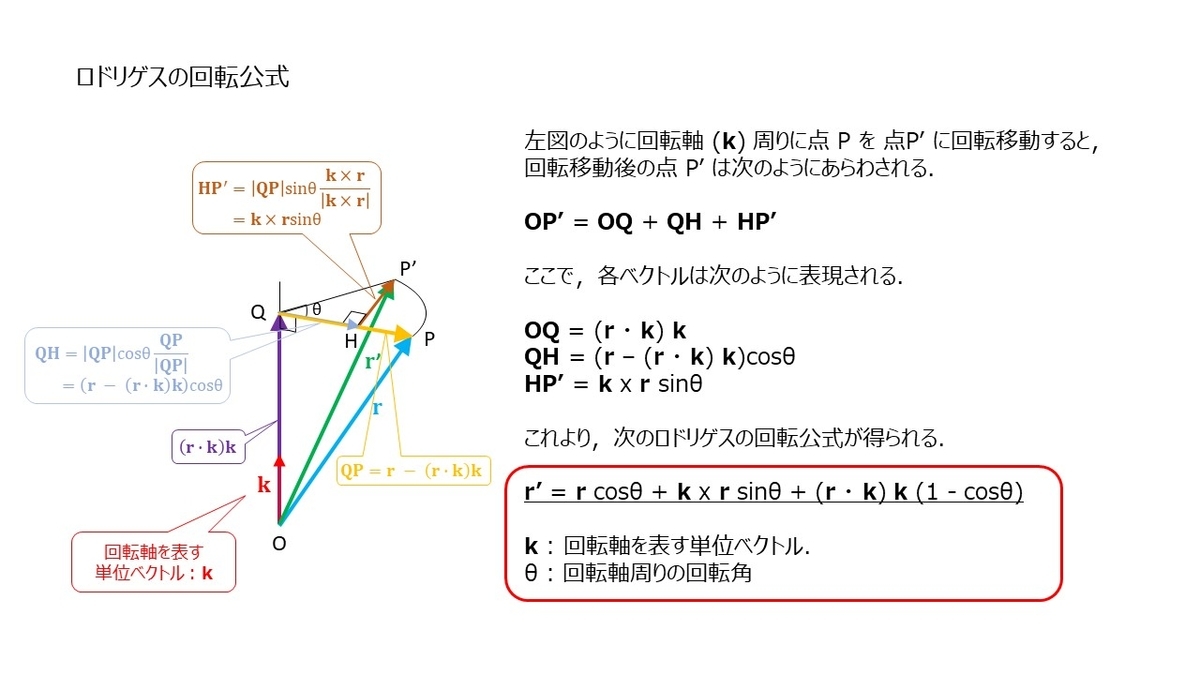
ロドリゲスの公式で,回転前の点 r を回転後の点 r' に変換させることができました.一方で,この回転と等価の回転行列 R を使っても点は変換できる(r' = Rr) となるはずなので,ロドリゲスの公式から等価な回転行列を求めます.ベクトルの外積計算を表現するために,外積計算用の行列を導入しています.

ということで,回転行列を回転軸と回転角を使って表現できるようになりました.が,回転軸と回転角で変数が計4つあります.もう一つ減らしたい...ということで,減らします.ここまでは回転軸ベクトルは単位ベクトルでしたが,回転軸ベクトルの大きさを回転角とすることによって変数を3つにします.

ふ~.できました.が,このままだと回転角が小さい,もしくは0の時に式が不定になってしまいます.つまり,回転角が0の時がこの表現方法の特異点ということになりますが,このままではまずいので,次にこれを除去します.
目次のページ
バンドル調整はシリーズ物として書いてまして,目次は下記のページになります.
daily-tech.hatenablog.com
